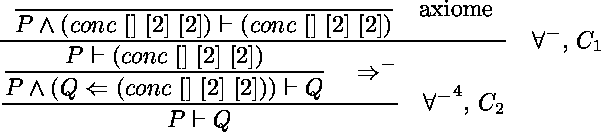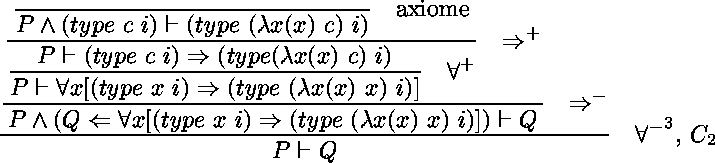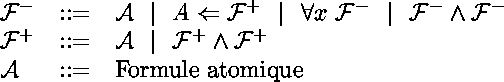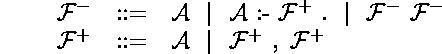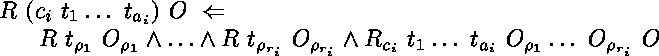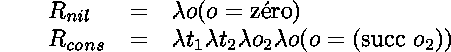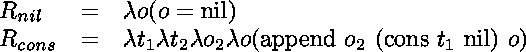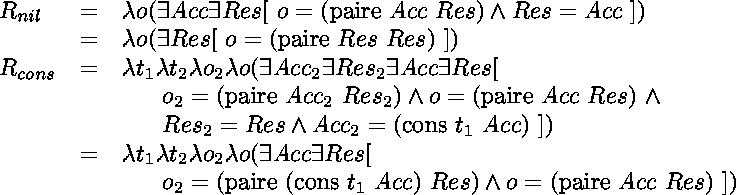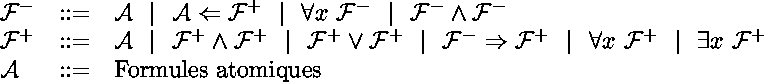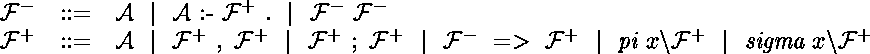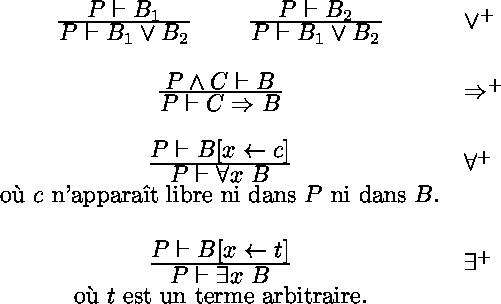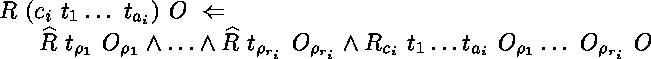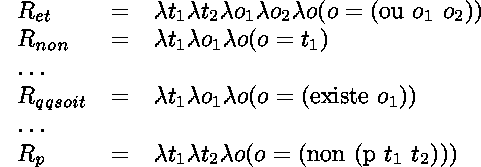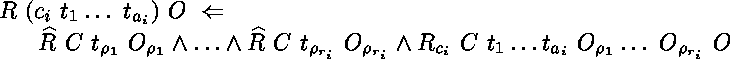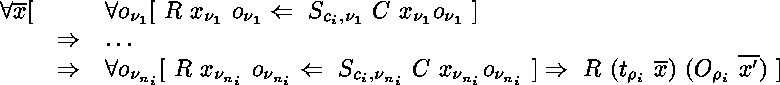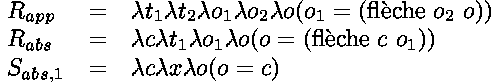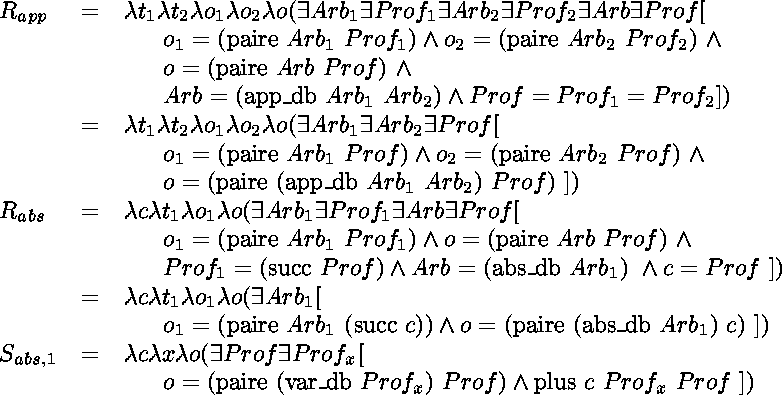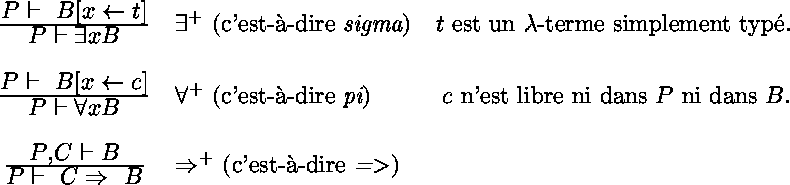Best viewed in 24pt and full-screen




Next: Q
Up: A-Z
Previous: O
type plus ((A->A)->A->A) -> ((A->A)->A->A) -> ((A->A)->A->A) -> o .
plus X Y s z
z (X s (Y s z)) .
(X s (Y s z)) .
Addition des entiers de Church.
 Partage de représentation.
n.m.
Désigne le fait de reconnaître que des objets d'origines distinctes
sont équivalents,
et de les faire partager une représentation commune.
C'est un complément indispensable du ramasse-miette pour
obtenir une gestion de mémoire efficace.
En
Partage de représentation.
n.m.
Désigne le fait de reconnaître que des objets d'origines distinctes
sont équivalents,
et de les faire partager une représentation commune.
C'est un complément indispensable du ramasse-miette pour
obtenir une gestion de mémoire efficace.
En  Prolog,
le partage est crucial pour la
Prolog,
le partage est crucial pour la  -réduction* et
pour l´unification*
[Brisset et Ridoux 92b, Brisset et Ridoux 92a].
La
-réduction* et
pour l´unification*
[Brisset et Ridoux 92b, Brisset et Ridoux 92a].
La  -réduction doit conserver les partages des termes dupliqués
et l'unification doit
mettre en
-réduction doit conserver les partages des termes dupliqués
et l'unification doit
mettre en  uvre les partages qu'elle cause.
uvre les partages qu'elle cause.
La réduction de graphe* permet naturellement de partager les
représentation
et on peut encore améliorer cet aspect en prenant en considération la
nature des termes qui forment un  -rédex :
combinateurs* ou
-rédex :
combinateurs* ou  -rédex*.
-rédex*.
La logique de l'unification est de trouver une substitution qui rend deux termes
égaux.
Celle de la recherche de la preuve est d'appliquer ces substitutions
au fur et à mesure où elles sont calculées.
Cela a pour effet de rendre de plus en plus de termes égaux.
Cela n'est pas un argument de terminaison car il se crée aussi
toujours de nouveaux termes.
Si deux termes sont égaux,
ils peuvent alors partager la même représentation.
Ce n'est pas fait dans les
mises en  uvre standard de Prolog car cela
complique un peu la représentation,
mais cela est naturel en
uvre standard de Prolog car cela
complique un peu la représentation,
mais cela est naturel en  car
la représentation des
car
la représentation des  -termes*
contient naturellement les mécanismes nécessaires.
L'effet est de substituer,
réversiblement car toute unification peut être annulée au retour-arrière,
un des termes à l'autre.
Cela économise de futures unifications car l'identité est plus facile
à tester que l'unifiabilité.
Cela économise aussi de la mémoire,
et donc le temps de la récupérer.
-termes*
contient naturellement les mécanismes nécessaires.
L'effet est de substituer,
réversiblement car toute unification peut être annulée au retour-arrière,
un des termes à l'autre.
Cela économise de futures unifications car l'identité est plus facile
à tester que l'unifiabilité.
Cela économise aussi de la mémoire,
et donc le temps de la récupérer.
Les termes d'un problème d'unification doivent être en forme de tête
expansée pour pouvoir être comparés.
Après l'application des substitutions produites par
imitation* ou projection*,
le terme qui était flexible,
et peut ne plus l'être,
n'est plus en forme de tête expansée.
Cependant,
sa nouvelle forme normale de tête
 -longue peut être déduite aisément du terme original et de la
substitution sans avoir recours à la procédure de
-longue peut être déduite aisément du terme original et de la
substitution sans avoir recours à la procédure de
 -réduction*.
Ce faisant,
imitation et projections inventent une substitution,
l'appliquent au terme flexible,
calculent sa nouvelle forme normale de tête
-réduction*.
Ce faisant,
imitation et projections inventent une substitution,
l'appliquent au terme flexible,
calculent sa nouvelle forme normale de tête  -longue
et la substituent au terme original.
-longue
et la substituent au terme original.
Par exemple,
le problème d'unification 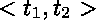 ,
où
,
où 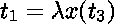 ,
,
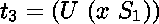 ,
et
,
et 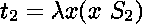 ,
produit trois substitutions après une application de la procédure
,
produit trois substitutions après une application de la procédure
 * :
* :
-
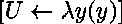 (projection),
(projection), -
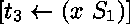 (forme normale de tête
(forme normale de tête  -longue de
-longue de 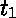 ),
), -
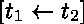 (partage de représentation).
(partage de représentation).
On voit donc qu'en plus plus des substitutions solutions,
beaucoup d'autres sont effectuées pour économiser du temps d'unification et de
 -réduction,
et de la mémoire.
-réduction,
et de la mémoire.
 Pertinent.
adj.
(rel. unificateur* et substitution*)
(en anglais, relevant)
Se dit d'un unificateur dont le domaine et le codomaine ne contiennent
que des variables des termes unifiés.
Par exemple,
étant donnés deux termes
Pertinent.
adj.
(rel. unificateur* et substitution*)
(en anglais, relevant)
Se dit d'un unificateur dont le domaine et le codomaine ne contiennent
que des variables des termes unifiés.
Par exemple,
étant donnés deux termes 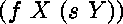 et
et
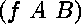 ,
l'unificateur
,
l'unificateur
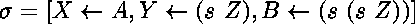 n'est pas pertinent
(à cause de la variable
n'est pas pertinent
(à cause de la variable  ),
mais l'unificateur
),
mais l'unificateur
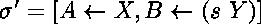 l'est.
l'est.
Au premier ordre,
et si un unificateur existe,
on peut toujours le choisir pertinent,
mais à l'ordre supérieur ce n'est pas toujours possible
( imitation* et projection*).
imitation* et projection*).
 pi.
synt.progr.
Notation concrète du quantificateur universel,
pi.
synt.progr.
Notation concrète du quantificateur universel,  , en
, en  Prolog.
C'est une réminiscence de la notation introduite par
Charles S. Peirce vers 1880 [Peirce 60].
Peirce voyait dans la quantification universelle une conjonction
généralisée
(élément neutre : vrai ou 1) et donc un produit,
Prolog.
C'est une réminiscence de la notation introduite par
Charles S. Peirce vers 1880 [Peirce 60].
Peirce voyait dans la quantification universelle une conjonction
généralisée
(élément neutre : vrai ou 1) et donc un produit,  .
.
Similairement, la notation concrète du quantificateur existentiel,
 , est sigma puisqu'on peut y voir une disjonction généralisée
(élément neutre : faux ou 0) et donc une somme,
, est sigma puisqu'on peut y voir une disjonction généralisée
(élément neutre : faux ou 0) et donc une somme,  .
.
L'usage de  et
et  est aussi attesté dans des écrits plus modernes
(par exemple [Church 40, Horn 51]).
est aussi attesté dans des écrits plus modernes
(par exemple [Church 40, Horn 51]).
 Pile de recherche.
n.f.
(syn. continuation d´échec*)
Structure de données associée au parcours d'un arbre de recherche
en profondeur d'abord
et avec retour arrière chronologique.
On y range la description des choix faits lors du parcours :
situation lors du choix et clause choisie.
Plus précisément,
on ne note pas explicitement la situation lors du choix,
mais un moyen d'y revenir à partir de la situation où on décide un retour
arrière.
Pile de recherche.
n.f.
(syn. continuation d´échec*)
Structure de données associée au parcours d'un arbre de recherche
en profondeur d'abord
et avec retour arrière chronologique.
On y range la description des choix faits lors du parcours :
situation lors du choix et clause choisie.
Plus précisément,
on ne note pas explicitement la situation lors du choix,
mais un moyen d'y revenir à partir de la situation où on décide un retour
arrière.
Dans  *,
la pile de recherche est complètement réalisée par
*,
la pile de recherche est complètement réalisée par  *.
Il faut noter que dans cette réalisation,
elle n'a de pile que la logique d'empilement et dépilement.
*.
Il faut noter que dans cette réalisation,
elle n'a de pile que la logique d'empilement et dépilement.
 Polarité.
n.f.
Le connecteur d'implication introduit une notion de polarité.
Si on donne un signe, + ou -, à une formule dont le connecteur
principal est l'implication,
la sous-formule de droite (la conclusion) aura le même signe,
alors que la sous-formule de gauche (l'hypothèse) aura le signe opposé.
La négation inverse aussi la polarité,
mais elle est absente des travaux présentés ici.
Les autres connecteurs et quantificateurs conservent la polarité.
Polarité.
n.f.
Le connecteur d'implication introduit une notion de polarité.
Si on donne un signe, + ou -, à une formule dont le connecteur
principal est l'implication,
la sous-formule de droite (la conclusion) aura le même signe,
alors que la sous-formule de gauche (l'hypothèse) aura le signe opposé.
La négation inverse aussi la polarité,
mais elle est absente des travaux présentés ici.
Les autres connecteurs et quantificateurs conservent la polarité.
On peut coder en  -calcul simplement typé*
les polarités et l'opérateur d'inversion de polarité.
-calcul simplement typé*
les polarités et l'opérateur d'inversion de polarité.
PLUS = v f
f v
v
MOINS = v f
f f
f
INV = p v
v f
f (p f v)
(p f v)
La flèche des types introduit la même notion de polarité.
Cela constitue un des aspects de la
correspondance de Curry-Howard*.
La polarité dans les types est à la base de la notion de
type inductif*.
 Portées de symboles et d´objets.
n.f.
Le mot «portée» résume les nouvelles capacités de
Portées de symboles et d´objets.
n.f.
Le mot «portée» résume les nouvelles capacités de  Prolog.
L'abstraction délimite la portée des variables dans les termes.
Les quantifications délimitent la portée des variables dans les formules.
Enfin,
les règles de déduction pour la quantification universelle et
l'implication dans les buts délimitent respectivement la portée des constantes
et des clauses dans les preuves.
Prolog.
L'abstraction délimite la portée des variables dans les termes.
Les quantifications délimitent la portée des variables dans les formules.
Enfin,
les règles de déduction pour la quantification universelle et
l'implication dans les buts délimitent respectivement la portée des constantes
et des clauses dans les preuves.
 Positif.
adj.
(ant. négatif*)
Positif.
adj.
(ant. négatif*)
1)
( polarité*)
polarité*)
2)
Se dit d'un
littéral* constitué d'une
formule atomique*.
 Premier ordre.
n.m.
(ant. ordre supérieur*)
Désigne une structure hiérarchique où les seules quantifications
possibles à un niveau de la hiérarchie ont pour domaine des objets
de niveau inférieur.
Par exemple,
une logique du premier ordre comprend des termes sans quantification
au niveau le plus bas
et des formules éventuellement quantifiées sur les termes,
et un langage de programmation fonctionnel de premier ordre comprend des termes
sans quantification au niveau le plus bas
et des fonctions de ces termes au-dessus.
Premier ordre.
n.m.
(ant. ordre supérieur*)
Désigne une structure hiérarchique où les seules quantifications
possibles à un niveau de la hiérarchie ont pour domaine des objets
de niveau inférieur.
Par exemple,
une logique du premier ordre comprend des termes sans quantification
au niveau le plus bas
et des formules éventuellement quantifiées sur les termes,
et un langage de programmation fonctionnel de premier ordre comprend des termes
sans quantification au niveau le plus bas
et des fonctions de ces termes au-dessus.
Prolog* est un langage de
premier ordre même s'il permet des constructions
qui semblent appartenir à l'ordre supérieur.
Par exemple,
on peut passer en paramètre d'un prédicat Prolog un
but*,
mais il faut bien voir que ce but doit plutôt être considéré comme un terme
de premier ordre qui est interprété comme un but.
L'ordre supérieur de Prolog permet seulement de ne pas écrire l'interpréteur
puisqu'il existe déjà.
 Prémisse.
n.f.
Prémisse.
n.f.
1)
( règle de déduction*)
règle de déduction*)
2)
Partie d'une implication qui joue le rôle de l'hypothèse.
 Prénexe.
adj.
Se dit d'une formule où toutes les quantifications sont à l'extérieur.
La formule sans les quantifications s'appelle la matrice.
Prénexe.
adj.
Se dit d'une formule où toutes les quantifications sont à l'extérieur.
La formule sans les quantifications s'appelle la matrice.
S'emploie pour des formules logiques et aussi pour les types.
Les types de  sont des formules prénexes* car la quantification des
variables de type se fait à l'extérieur des types.
sont des formules prénexes* car la quantification des
variables de type se fait à l'extérieur des types.
 Prescriptif.
adj.
(ant. descriptif*)
Se dit d'un typage
à la Church* des programmes Prolog*.
Une discipline de typage est définie a priori
et on ne donne un sens qu'aux programmes bien typés.
On peut souhaiter que les types soient inférés pour libérer le programmeur
d'une tâche automatisable,
ou au contraire qu'ils soient déclarés pour forcer le programmeur à écrire
les spécifications élémentaires de l'application développée.
Dans ce domaine,
les propositions techniques consistent souvent en des adaptations
à la programmation logique de disciplines de typage inventées pour la
programmation fonctionnelle ou le
Prescriptif.
adj.
(ant. descriptif*)
Se dit d'un typage
à la Church* des programmes Prolog*.
Une discipline de typage est définie a priori
et on ne donne un sens qu'aux programmes bien typés.
On peut souhaiter que les types soient inférés pour libérer le programmeur
d'une tâche automatisable,
ou au contraire qu'ils soient déclarés pour forcer le programmeur à écrire
les spécifications élémentaires de l'application développée.
Dans ce domaine,
les propositions techniques consistent souvent en des adaptations
à la programmation logique de disciplines de typage inventées pour la
programmation fonctionnelle ou le
 -calcul* [Mycroft et O'Keefe 84, Lakshman et Reddy 91, Hill et Topor 92, Louvet et Ridoux 96].
-calcul* [Mycroft et O'Keefe 84, Lakshman et Reddy 91, Hill et Topor 92, Louvet et Ridoux 96].
 Preuve constructive.
n.f.
Preuve suffisamment explicite pour contenir la description d'un terme
vérifiant la propriété prouvée.
La preuve constructive d'une disjonction,
Preuve constructive.
n.f.
Preuve suffisamment explicite pour contenir la description d'un terme
vérifiant la propriété prouvée.
La preuve constructive d'une disjonction,  ,
est donnée par la preuve d'un de ses membres,
,
est donnée par la preuve d'un de ses membres,
 ou
ou  ,
tandis que la preuve constructive d'une existentielle,
,
tandis que la preuve constructive d'une existentielle,  est donnée par une preuve de la formule où un terme remplace la
variable quantifiée,
est donnée par une preuve de la formule où un terme remplace la
variable quantifiée,  .
.
L'exemple typique de preuve non-constructive est le suivant :
Soit à prouver qu'il existe
deux irrationnels  et
et  ,
tels que
,
tels que 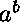 est rationnel.
est rationnel.
Posons 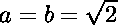 .
Si
.
Si 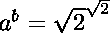 est rationnel, la preuve est faite.
est rationnel, la preuve est faite.
Sinon, 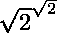 est irrationnel.
Posons
est irrationnel.
Posons 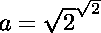 et
et 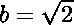 .
.
Alors 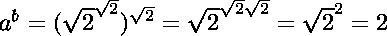 est rationnel, la preuve est faite.
est rationnel, la preuve est faite.
Cette démonstration ne montre pas comment construire  et
et  ,
tels que
,
tels que 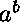 est rationnel.
est rationnel.
La programmation logique exploite la recherche d'une preuve constructive
comme un mécanisme de calcul.
Dans ce cadre,
les résultats sont les valeurs qu'il faut substituer aux variables existentielles
de la formule pour la prouver.
 Preuve uniforme.
n.f.
Preuve du calcul des séquents*
qui est telle que les parties droites
de tous les séquents conclusions d'une règle d'introduction à gauche
sont atomiques.
Preuve uniforme.
n.f.
Preuve du calcul des séquents*
qui est telle que les parties droites
de tous les séquents conclusions d'une règle d'introduction à gauche
sont atomiques.
La prouvabilité uniforme n'est pas complète pour la prouvabilité
intuitionniste en général,
mais elle l'est pour certains fragments syntaxiques.
Par exemple,
elle est complète pour le fragment des clauses de Horn.
Par exemple,
soit  le programme formé des clauses
le programme formé des clauses
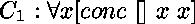 et
et
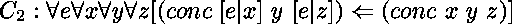 ,
soit
,
soit 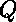 le but
le but 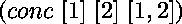 ,
une preuve uniforme de
,
une preuve uniforme de 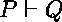 est comme suit :
est comme suit :
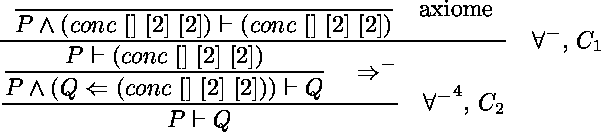
La règle étiquetée 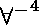 est un raccourci pour 4 applications de la règle
est un raccourci pour 4 applications de la règle  dans laquelle les variables universellement quantifiées
dans laquelle les variables universellement quantifiées
 ,
,  ,
,  et
et  sont remplacées par
sont remplacées par
 ,
,  ,
, 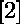 et
et 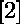 .
.
En fait,
la complétude pour le fragment des clauses de Horn n'a qu'un
intérêt relatif car prouvabilité classique et prouvabilité
intuitionniste coïncident pour ce fragment,
et on connaît déjà des stratégies dirigées par le but
qui sont complètes pour ce fragment
(par exemple, la 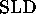 -résolution).
La prouvabilité uniforme est aussi complète pour le fragment
des formules héréditaires de Harrop.
Cette fois-ci c'est important et cela va donner la sémantique
opérationnelle de
-résolution).
La prouvabilité uniforme est aussi complète pour le fragment
des formules héréditaires de Harrop.
Cette fois-ci c'est important et cela va donner la sémantique
opérationnelle de  Prolog.
Prolog.
Par exemple,
soit  le programme formé des clauses
le programme formé des clauses
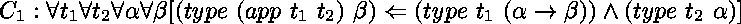 et
et
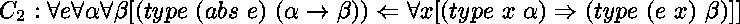 ,
,
soit 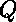 le but
le but
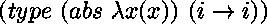 ,
une preuve uniforme de
,
une preuve uniforme de 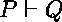 est comme suit :
est comme suit :
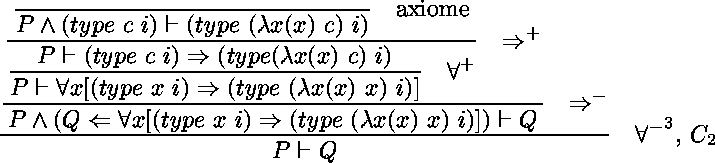
La règle étiquetée 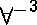 est un raccourci pour 3 applications de la règle
est un raccourci pour 3 applications de la règle  dans laquelle les variables universellement
quantifiées
dans laquelle les variables universellement
quantifiées  ,
,  et
et  sont remplacées par
sont remplacées par
 ,
,  et
et  .
.
 Préunificateur.
n.m.
(rel. unificateur*)
Étant donnée une instance d'un problème
d´unification*,
un préunificateur est une substitution*
telle que si on l'applique à l'instance de problème d'unification,
il en résulte une autre instance de problème d'unification
constituée uniquement de paires flexible-flexible*.
Préunificateur.
n.m.
(rel. unificateur*)
Étant donnée une instance d'un problème
d´unification*,
un préunificateur est une substitution*
telle que si on l'applique à l'instance de problème d'unification,
il en résulte une autre instance de problème d'unification
constituée uniquement de paires flexible-flexible*.
Il existe un préunificateur si et seulement si il existe un unificateur.
Dans le cas de l'unification d'ordre supérieur,
la différence est que les préunificateurs sont plus faciles à énumérer que les
unificateurs.
 Programmation logique.
n.f.
La programmation logique est un paradigme de programmation où les
programmes sont des formules logiques et les exécuter revient à
rechercher leur preuve.
La mise en
Programmation logique.
n.f.
La programmation logique est un paradigme de programmation où les
programmes sont des formules logiques et les exécuter revient à
rechercher leur preuve.
La mise en  uvre la plus populaire de ce paradigme est
Prolog*,
qui est fondé sur le formalisme des clauses de Horn.
Même si ce formalisme est calculatoirement
complet [Andréka et Németi 76, Tärnlund 77, Lloyd 88],
on a souvent essayé de l'augmenter afin de gagner en flexibilité
et en expressivité.
Un de ces essais est
uvre la plus populaire de ce paradigme est
Prolog*,
qui est fondé sur le formalisme des clauses de Horn.
Même si ce formalisme est calculatoirement
complet [Andréka et Németi 76, Tärnlund 77, Lloyd 88],
on a souvent essayé de l'augmenter afin de gagner en flexibilité
et en expressivité.
Un de ces essais est
 Prolog* [Miller et Nadathur 86b, Miller et al. 87].
Prolog* [Miller et Nadathur 86b, Miller et al. 87].
On considère généralement Colmerauer*
et Kowalski comme les co-inventeurs du paradigme [Cohen 88],
le premier pour être l'inventeur du principe et avoir dirigé l'implémentation
originale [Battani et Meloni 73],
le second pour avoir établi le rapport avec le calcul des prédicats et
les relations entre la sémantique déclarative de Prolog et sa sémantique
procédurale [Kowalski 74, Kowalski et Van Emden 76].
 Projection.
n.f.
Une des opérations élémentaires
du semi-algorithme de Huet*.
Projection.
n.f.
Une des opérations élémentaires
du semi-algorithme de Huet*.
Étant donnée une paire
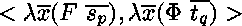 ,
où
,
où  est une tête flexible*
(une variable logique)
et
est une tête flexible*
(une variable logique)
et 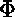 est une tête rigide*
(pas une variable logique),
pour chaque
est une tête rigide*
(pas une variable logique),
pour chaque 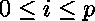 tel que
tel que
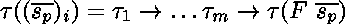 ,
la règle de projection produit
,
la règle de projection produit
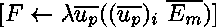 .
Chaque
.
Chaque  est une application
est une application  ,
où
,
où  est une variable logique nouvelle et d'un type approprié.
est une variable logique nouvelle et d'un type approprié.
Après application de la substitution,
de la  -réduction*
et de la simplification*,
le problème se ramène à résoudre les paires
-réduction*
et de la simplification*,
le problème se ramène à résoudre les paires
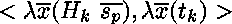 pour chaque
pour chaque 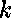 .
.
Ici,
et au contraire de l´imitation*,
on tente de trouver un paramètre de  qui produirait un
qui produirait un 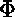 .
Cependant,
.
Cependant,
 et son paramètre ne peuvent pas être du même type.
On va donc devoir «habiller» le paramètre de manière
à obtenir un terme compatible avec
et son paramètre ne peuvent pas être du même type.
On va donc devoir «habiller» le paramètre de manière
à obtenir un terme compatible avec  .
Cela se fait comme pour l'imitation.
L'introduction des
.
Cela se fait comme pour l'imitation.
L'introduction des  fait aussi qu'il n'est pas toujours possible
de trouver un unificateur pertinent*.
fait aussi qu'il n'est pas toujours possible
de trouver un unificateur pertinent*.
Pour savoir tester la précondition de la règle de projection,
il faut et il suffit
que les variables logiques soient représentées avec leur types,
et que les types oubliés*
soient effectivement passés en paramètre.
C'est un point fondamental qui fait perdre de l'intérêt aux
théorèmes de correction sémantique qui permettent d'éliminer
complètement les types de la représentation.
On a plutôt besoin de savoir quel est le minimum de types qu'il faut
représenter pour les propager correctement vers les variables
logiques [Brisset et Ridoux 92b].
 Prolog.
Langage de programmation logique fondé sur la logique des
clauses de Horn*.
Une norme
Prolog.
Langage de programmation logique fondé sur la logique des
clauses de Horn*.
Une norme 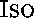 existe sous le nom de Standard Prolog
(
existe sous le nom de Standard Prolog
( /
/ 13211 [Deransart et al. 96]).
13211 [Deransart et al. 96]).
Un programme Prolog est fait de clauses*
( )
et de buts*
(
)
et de buts*
( )
selon la syntaxe logique suivante :
)
selon la syntaxe logique suivante :
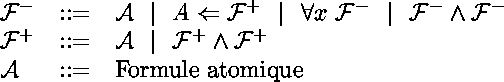
Dans la syntaxe concrète les quantifications universelles sont implicites :
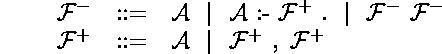
Règles de déduction :

On pourrait craindre que la restriction aux clauses de Horn limite la
puissance de calcul,
mais il n'en est
rien [Andréka et Németi 76, Tärnlund 77].
Un résultat récent montre qu'on peut restreindre encore les
clauses de Horn sans perdre de puissance de
calcul [Devienne et al. 96].
 Prolog typé (induction structurelle en).
n.f.
(rel. induction structurelle*)
L'induction structurelle en Prolog typé se formalise de la manière suivante.
Soit à définir une relation
Prolog typé (induction structurelle en).
n.f.
(rel. induction structurelle*)
L'induction structurelle en Prolog typé se formalise de la manière suivante.
Soit à définir une relation  de type
de type 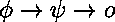 par
induction structurelle sur l'argument de type
par
induction structurelle sur l'argument de type 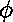 .
L'argument de type
.
L'argument de type 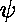 est appelé le «résultat»
et il est noté
est appelé le «résultat»
et il est noté 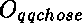 ou
ou 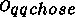 .
Aux constructeurs
.
Aux constructeurs 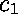 , ...,
, ..., 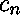 du type
du type 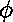 sont associées
des relations
sont associées
des relations 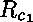 , ...,
, ..., 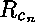 ,
telles que la relation à définir,
,
telles que la relation à définir,
 ,
le soit par des règles de la forme
,
le soit par des règles de la forme
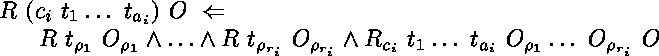
où 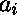 est l'arité de
est l'arité de 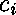 ,
,
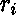 est le nombre d'arguments de
est le nombre d'arguments de 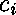 qui ont le type
qui ont le type 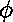 et les
et les 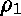 , ...,
, ..., 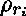 sont leurs rangs.
sont leurs rangs.
Ces règles sont entièrement déterminées par le type 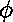 (et ses constructeurs)
et les relations
(et ses constructeurs)
et les relations 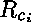 .
Une relation de type fixé,
.
Une relation de type fixé, 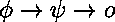 ,
supposée définissable par induction structurelle sur
,
supposée définissable par induction structurelle sur 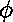 ,
est donc entièrement déterminée par les
,
est donc entièrement déterminée par les 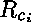 .
Un programmeur peut les composer «à la main»,
mais on peut aussi imaginer de les calculer à partir d'exemples.
Le squelette des règles peut être produit automatiquement d'après le type
(
.
Un programmeur peut les composer «à la main»,
mais on peut aussi imaginer de les calculer à partir d'exemples.
Le squelette des règles peut être produit automatiquement d'après le type
( itérateur*).
itérateur*).
Des raffinements sont nécessaires pour augmenter la flexibilité du schéma,
permettre des définitions mutuellement récursives
et prendre en compte le polymorphisme,
mais cette définition suffit à formaliser l'induction structurelle
en programmation logique du premier ordre.
Par exemple,
étant donné le type des listes* homogènes,
la relation qui associe une liste à sa longueur est définie par
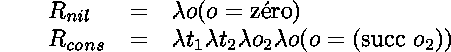
En notation  Prolog,
ces deux relations plus le type list déterminent le prédicat
Prolog,
ces deux relations plus le type list déterminent le prédicat
longueur nil O :- O = zéro .
longueur (cons T1 T2) O :- longueur T2 O2 , O = (succ O2) .
qui peut être simplifié pour produire le prédicat attendu.
De la même façon,
le renversement naïf de liste est défini par les relations
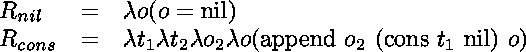
et le renversement non-naïf est défini par les relations
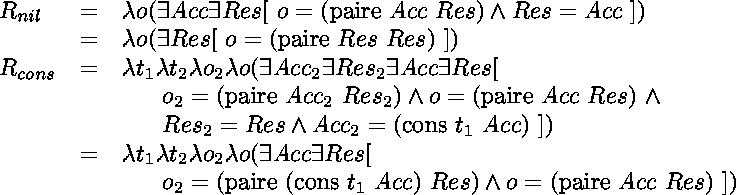
Il a fallu «empaqueter» dans une paire le résultat proprement dit de
l'inversion de liste et l'accumulateur.
On utilise aussi d'une manière critique la spécificité de la programmation
logique que constituent les variables existentielles.
Les deux dernières relations déterminent le prédicat
nrev nil O :- sigma Res (O = (paire Res Res)) .
(O = (paire Res Res)) .
nrev (cons T1 T2) O :-
nrev T2 O2 ,
sigma Acc (sigma Res
(sigma Res ( O2 = (paire (cons T1 Acc) Res) , O = (paire Acc Res) )) .
( O2 = (paire (cons T1 Acc) Res) , O = (paire Acc Res) )) .
qui se simplifie en
nrev nil (paire Res Res) .
nrev (cons T1 T2) (paire Acc Res) :- nrev T2 (paire (cons T1 Acc) Res) .
Au premier ordre tout se passe comme si le calcul consistait dans
le remplacement des occurrences de constructeurs du type considéré
par des opérateurs définis par les relations 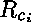 ,
et cela suffit pour associer une valeur à tous les sous-termes qui
ont le type considéré.
,
et cela suffit pour associer une valeur à tous les sous-termes qui
ont le type considéré.

 Prolog.
(
Prolog.
( historique de
historique de  Prolog*)
La définition de
Prolog*)
La définition de  Prolog peut être schématisée par l'équation suivante :
Prolog peut être schématisée par l'équation suivante :
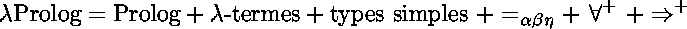
Le domaine de calcul de  Prolog est celui des termes du
Prolog est celui des termes du
 -calcul simplement typé*.
Les notations
-calcul simplement typé*.
Les notations  et
et  indiquent que les connecteurs
indiquent que les connecteurs
 et
et  sont admis dans les buts.
Ils s'ajoutent à la conjonction des buts de Prolog :
sont admis dans les buts.
Ils s'ajoutent à la conjonction des buts de Prolog :
 (notée «,»).
Les connecteurs admis à construire des clauses sont les mêmes qu'en Prolog :
(notée «,»).
Les connecteurs admis à construire des clauses sont les mêmes qu'en Prolog :
 et
et  ,
dont les occurrences les plus externes sont implicites,
et
,
dont les occurrences les plus externes sont implicites,
et  ,
qui est explicite
(noté :-).
,
qui est explicite
(noté :-).
Syntaxe logique :
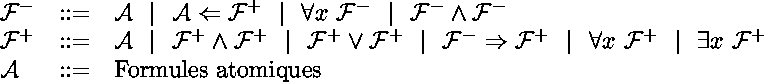
Syntaxe concrète approchée
(les quantifications universelles les plus externes de  sont implicites) :
sont implicites) :
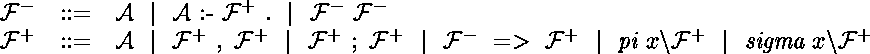
Règles de déduction spécifiques :
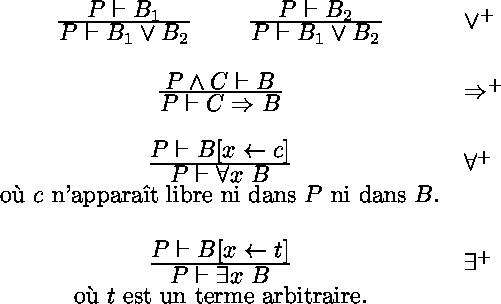
Cette extension du langage des termes et de
celui des formules de Prolog conserve
des propriétés logiques et calculatoires
intéressantes [Miller et Nadathur 86b, Miller et al. 87]
( preuve uniforme*).
preuve uniforme*).

 Prolog (difficultés de).
n.f.
La programmation en
Prolog (difficultés de).
n.f.
La programmation en  Prolog recèle quelques pièges dont nous listons ici
quelques uns des plus spécifiques.
Prolog recèle quelques pièges dont nous listons ici
quelques uns des plus spécifiques.
x E :
L'expression
x
E :
L'expression
x E ne désigne pas une
E ne désigne pas une  -expression
dont on ne sait rien si ce n'est qu'elle lie une variable x.
Elle désigne une
-expression
dont on ne sait rien si ce n'est qu'elle lie une variable x.
Elle désigne une  -expression dont on sait que la variable qu'elle lie
n'est pas utilisée dans le corps.
Ce piège n'est pas une construction académique.
Les débutants tombent dedans,
et il existe un livre consacré aux techniques de programmation logique appliquées
au traitement de la langue naturelle qui
contient systématiquement l'erreur lorsqu'il
est question de
-expression dont on sait que la variable qu'elle lie
n'est pas utilisée dans le corps.
Ce piège n'est pas une construction académique.
Les débutants tombent dedans,
et il existe un livre consacré aux techniques de programmation logique appliquées
au traitement de la langue naturelle qui
contient systématiquement l'erreur lorsqu'il
est question de  Prolog
[Citation omise intentionnellement].
Prolog
[Citation omise intentionnellement].
Comme tous les calculs se font modulo la
 -équivalence*,
tenter de déterminer le nom d'une variable liée n'a pas de sens,
et tenter de capturer le corps d'une abstraction
où une
-équivalence*,
tenter de déterminer le nom d'une variable liée n'a pas de sens,
et tenter de capturer le corps d'une abstraction
où une  -variable serait libre n'en a pas non plus.
-variable serait libre n'en a pas non plus.
(A B) :
L'expression
(A B) ne permet pas de discriminer les termes formés par une
application,
et encore moins de capturer les deux membres de l'application.
Comme tous les calculs se font modulo la
 -équivalence*,
tenter de déterminer la formation syntaxique d'un terme n'a pas de sens.
Par exemple,
(A B) est unifiable
(modulo les types)
avec 72, x
-équivalence*,
tenter de déterminer la formation syntaxique d'un terme n'a pas de sens.
Par exemple,
(A B) est unifiable
(modulo les types)
avec 72, x x et (f 1),
et dans ce dernier cas les substitutions solutions
x et (f 1),
et dans ce dernier cas les substitutions solutions
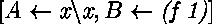 ,
,
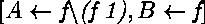 et
et
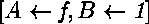 sont également correctes.
Les débutants tombent fréquemment dans ce piège.
Si on connaît la liste des constantes fonctionnelles qui sont utilisées,
on peut sélectionner la solution recherchée en précisant que A
est dans cette liste.
Sinon,
il faut avoir recours à une notation des termes plus explicite
(
sont également correctes.
Les débutants tombent fréquemment dans ce piège.
Si on connaît la liste des constantes fonctionnelles qui sont utilisées,
on peut sélectionner la solution recherchée en précisant que A
est dans cette liste.
Sinon,
il faut avoir recours à une notation des termes plus explicite
( l_terme*).
l_terme*).
Cette remarque se généralise à toute tentative de discriminer des termes par
des propriétés qui ne sont pas stables par
 -réduction*.
Autre exemple,
la propriété d'être une composition de fonctions est significative au niveau
objet pour manipuler symboliquement des fonctions,
mais elle n'est pas stable par
-réduction*.
Autre exemple,
la propriété d'être une composition de fonctions est significative au niveau
objet pour manipuler symboliquement des fonctions,
mais elle n'est pas stable par
 -réduction ;
on doit donc la représenter de manière explicite.
-réduction ;
on doit donc la représenter de manière explicite.
r a b. r b a. q :- pi x (pi y
(pi y (r x y => r y x)) :
Vu le sous-ensemble de formules et le fragment de logique considérés en
(r x y => r y x)) :
Vu le sous-ensemble de formules et le fragment de logique considérés en  Prolog,
l'interprétation de la quantification universelle est
intentionnelle*.
Le but (pi x
Prolog,
l'interprétation de la quantification universelle est
intentionnelle*.
Le but (pi x (pi y
(pi y (r x y => r y x))) échoue donc
car il ne peut réussir que dans une logique extensionnelle*.
(r x y => r y x))) échoue donc
car il ne peut réussir que dans une logique extensionnelle*.
Des opérateurs extensionnels existent en  * sous la forme
des prédicats prédéfinis setof et findall.
* sous la forme
des prédicats prédéfinis setof et findall.
pi 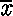
 (sigma Y
(sigma Y (...)) :
On a parfois besoin d'un nombre (que l'on croit) indéterminé de quantifications
universelles suivies d'une quantification existentielle.
L'exemple typique est celui du calcul de la clôture universelle
d'une formule lue.
Ce nombre dépend en général d'une structure de données.
On peut la parcourir pour connaître ce nombre
et ouvrir le bon nombre de quantifications dans une récursion.
On peut aussi se souvenir que
(...)) :
On a parfois besoin d'un nombre (que l'on croit) indéterminé de quantifications
universelles suivies d'une quantification existentielle.
L'exemple typique est celui du calcul de la clôture universelle
d'une formule lue.
Ce nombre dépend en général d'une structure de données.
On peut la parcourir pour connaître ce nombre
et ouvrir le bon nombre de quantifications dans une récursion.
On peut aussi se souvenir que
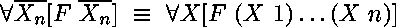 et n'ouvrir qu'une quantification universelle,
mais consommer des numéros de variables que l'on gère à l'aide de paramètres
supplémentaires :
(pi xs
et n'ouvrir qu'une quantification universelle,
mais consommer des numéros de variables que l'on gère à l'aide de paramètres
supplémentaires :
(pi xs (But xs 1 N)).
Cette méthode suppose que toutes les variables
de
(But xs 1 N)).
Cette méthode suppose que toutes les variables
de 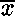 ont le même type.
ont le même type.
sigma 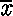
 (pi Y
(pi Y (...)) :
On a parfois besoin d'un nombre (que l'on croit encore)
indéterminé de quantifications existentielles
suivies d'une quantification universelle.
Ce nombre dépend en général d'une structure de données.
On peut la parcourir pour connaître ce nombre
et ouvrir le bon nombre de quantifications dans une récursion.
On peut aussi quantifier existentiellement
une liste non-déterminée de variables :
(sigma Xs
(...)) :
On a parfois besoin d'un nombre (que l'on croit encore)
indéterminé de quantifications existentielles
suivies d'une quantification universelle.
Ce nombre dépend en général d'une structure de données.
On peut la parcourir pour connaître ce nombre
et ouvrir le bon nombre de quantifications dans une récursion.
On peut aussi quantifier existentiellement
une liste non-déterminée de variables :
(sigma Xs (But Xs [])).
Leur appartenance à la liste Xs
garantit aux variables créées progressivement d'appartenir
au bon contexte de quantification.
On peut rendre la gestion de la liste de variables presque transparente en
utilisant les
(But Xs [])).
Leur appartenance à la liste Xs
garantit aux variables créées progressivement d'appartenir
au bon contexte de quantification.
On peut rendre la gestion de la liste de variables presque transparente en
utilisant les  * :
sigma_var But --> ` [X] & (But X).
Cette méthode suppose aussi que toutes les variables
de
* :
sigma_var But --> ` [X] & (But X).
Cette méthode suppose aussi que toutes les variables
de 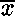 ont le même type.
Si elles n'ont pas toutes le même type,
mais que les types qu'elles ont sont connus à l'avance,
on peut encore utiliser cette technique
en «emballant» chaque X dans la liste par un constructeur qui indique
son type.
ont le même type.
Si elles n'ont pas toutes le même type,
mais que les types qu'elles ont sont connus à l'avance,
on peut encore utiliser cette technique
en «emballant» chaque X dans la liste par un constructeur qui indique
son type.

 Prolog (extensionnalité en).
n.f.
(rel. extensionnel* et extensionnalité fonctionnelle*)
Prolog (extensionnalité en).
n.f.
(rel. extensionnel* et extensionnalité fonctionnelle*)
 Prolog intègre l'axiome
de
Prolog intègre l'axiome
de  -équivalence*,
qui satisfait le principe d'extensionnalité fonctionnelle
pour le
-équivalence*,
qui satisfait le principe d'extensionnalité fonctionnelle
pour le  -calcul* pur,
et une interprétation intentionnelle*
de la quantification universelle.
-calcul* pur,
et une interprétation intentionnelle*
de la quantification universelle.
Il ne faut pas y voir de contradiction,
car le domaine de calcul de  Prolog n'est pas celui
du
Prolog n'est pas celui
du  -calcul pur,
mais celui du
-calcul pur,
mais celui du  -calcul simplement typé*,
pour lequel la
-calcul simplement typé*,
pour lequel la  -équivalence ne satisfait pas
complètement le principe d'extensionnalité fonctionnelle.
Donc,
-équivalence ne satisfait pas
complètement le principe d'extensionnalité fonctionnelle.
Donc,
 Prolog est une logique essentiellement intentionnelle,
que ce soit au niveau des quantifications et de la déduction,
ou au niveau des
Prolog est une logique essentiellement intentionnelle,
que ce soit au niveau des quantifications et de la déduction,
ou au niveau des  -termes et de la
-termes et de la  -équivalence.
-équivalence.

 Prolog (formules de).
n.f.
Ce sont des notations de formules héréditaires de Harrop*.
Dans les programmes,
les connecteurs
Prolog (formules de).
n.f.
Ce sont des notations de formules héréditaires de Harrop*.
Dans les programmes,
les connecteurs 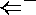 ,
,  et
et 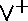 sont notés :- , «,» et «;» comme en Prolog.
Les connecteurs
sont notés :- , «,» et «;» comme en Prolog.
Les connecteurs  ,
,  ,
,  ,
propres à
,
propres à  Prolog,
sont notés => ,
pi* et sigma*.
Les connecteurs
Prolog,
sont notés => ,
pi* et sigma*.
Les connecteurs 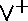 et
et  peuvent être considérés
comme dérivés des autres.
Nous les mentionnons pourtant dans la syntaxe car ils permettent d'alléger
l'écriture des programmes.
La nouveauté de
peuvent être considérés
comme dérivés des autres.
Nous les mentionnons pourtant dans la syntaxe car ils permettent d'alléger
l'écriture des programmes.
La nouveauté de  Prolog par rapport à Prolog est dans le langage des
buts* :
ils peuvent contenir des quantifications explicites,
universelles et existentielles,
et des implications.
Prolog par rapport à Prolog est dans le langage des
buts* :
ils peuvent contenir des quantifications explicites,
universelles et existentielles,
et des implications.
En Prolog,
une variable libre dans une clause est considérée
quantifiée universellement au niveau de la clause.
Une des nouveautés de  Prolog est qu'une clause peut
apparaître imbriquée dans une autre.
Une variable peut donc être libre dans plusieurs clauses à la fois.
En fait,
la règle de reconstruction des quantifications de
Prolog est qu'une clause peut
apparaître imbriquée dans une autre.
Une variable peut donc être libre dans plusieurs clauses à la fois.
En fait,
la règle de reconstruction des quantifications de  Prolog est une extension
de celle de Prolog :
une variable libre est considérée
quantifiée universellement au niveau de la clause de plus grande portée
(c'est-à-dire la plus englobante).
Par ailleurs,
on peut lier explicitement une variable dans une clause imbriquée
en utilisant une quantification universelle explicite au niveau de cette clause.
On appelle ces variables et toutes celles qui sont introduites
par une quantification existentielle dans un but
les variables logiques*
ou les inconnues* de
Prolog est une extension
de celle de Prolog :
une variable libre est considérée
quantifiée universellement au niveau de la clause de plus grande portée
(c'est-à-dire la plus englobante).
Par ailleurs,
on peut lier explicitement une variable dans une clause imbriquée
en utilisant une quantification universelle explicite au niveau de cette clause.
On appelle ces variables et toutes celles qui sont introduites
par une quantification existentielle dans un but
les variables logiques*
ou les inconnues* de  Prolog.
Prolog.

 Prolog (historique de).
n.m.
Le développement des différentes facettes de
Prolog (historique de).
n.m.
Le développement des différentes facettes de  Prolog ne s'est pas fait d'un seul
coup.
Au contraire,
il s'est fait progressivement avec des motivations particulières qui
n'apparaissent pas immédiatement
quand on considère
Prolog ne s'est pas fait d'un seul
coup.
Au contraire,
il s'est fait progressivement avec des motivations particulières qui
n'apparaissent pas immédiatement
quand on considère  Prolog a posteriori.
Prolog a posteriori.
Le premier objectif de Dale Miller a été de concevoir une logique d'ordre
supérieur qui soit récursivement axiomatisable [Miller 83].
Il définit pour cela une variante de la théorie des types simples de
Church* [Church 40].
Cette logique a un fragment «à la Horn» qui constitue le premier système
 Prolog [Miller et Nadathur 86b, Nadathur 87].
Ce développement se fait dans une logique typée (évidemment) dans laquelle
des variables de type*
sont utilisées pour introduire une forme de polymorphisme.
Prolog [Miller et Nadathur 86b, Nadathur 87].
Ce développement se fait dans une logique typée (évidemment) dans laquelle
des variables de type*
sont utilisées pour introduire une forme de polymorphisme.
Son second objectif a été de formaliser logiquement la notion de module
et d'importation.
Miller observe que l´implication intuitionniste*
joue très bien ce rôle,
et il l'ajoute à
Prolog [Miller 86, Miller 89c].
Il observe aussi que l'implication seule ne permet pas de formaliser
la possibilité de cacher de l'information
qu'ont souvent les modules
( types abstraits*).
Miller montre que les quantifications
essentiellement universelles*
peuvent jouer ce rôle [Miller 89a, Miller 93].
Ces développements autour de la modularité se font dans une logique de
premier ordre et non-typée.
types abstraits*).
Miller montre que les quantifications
essentiellement universelles*
peuvent jouer ce rôle [Miller 89a, Miller 93].
Ces développements autour de la modularité se font dans une logique de
premier ordre et non-typée.
L'étape suivante est de reconnaître que la combinaison particulière
d'implications et de quantifications qui est utilisée correspond au fragment
héréditaire des
formules de Harrop [Miller et al. 87, Miller et al. 91]
( formules héréditaires de Harrop*).
Les dévelopement théoriques se font dans une logique typée sans polymorphisme,
mais le polymorphisme est ajouté dans la présentation concrète du langage.
Miller et ses collègues observent que les applications de
formules héréditaires de Harrop*).
Les dévelopement théoriques se font dans une logique typée sans polymorphisme,
mais le polymorphisme est ajouté dans la présentation concrète du langage.
Miller et ses collègues observent que les applications de  Prolog
dépassent largement la seule expression de la modularité:
traitement de la langue naturelle [Miller et Nadathur 86a, Pareschi et Miller 90],
manipulation de programmes et de formules [Miller et Nadathur 87],
et de leur syntaxe et leur sémantique [Miller 91a, Hannan et Miller 92],
et la démonstration automatique [Felty 87, Felty et Miller 88, Felty et Miller 90, Felty 93].
De nombreuses autres applications
ont été développées après celles de ces précurseurs
(voir la section «Applications»*).
Prolog
dépassent largement la seule expression de la modularité:
traitement de la langue naturelle [Miller et Nadathur 86a, Pareschi et Miller 90],
manipulation de programmes et de formules [Miller et Nadathur 87],
et de leur syntaxe et leur sémantique [Miller 91a, Hannan et Miller 92],
et la démonstration automatique [Felty 87, Felty et Miller 88, Felty et Miller 90, Felty 93].
De nombreuses autres applications
ont été développées après celles de ces précurseurs
(voir la section «Applications»*).
L´unification d´ordre supérieur* est
un problème semi-décidable* et infinitaire*,
et même si le semi-algorithme de Huet* se révèle
praticable,
une difficulté théorique subsiste.
Miller propose de la résoudre en substituant aux
 -termes simplement typés*
un fragment d'entre eux pour lequel l'unification est un problème décidable
et unitaire [Miller 89b, Miller 91b]
(
-termes simplement typés*
un fragment d'entre eux pour lequel l'unification est un problème décidable
et unitaire [Miller 89b, Miller 91b]
(
 *).
Miller montre aussi que le problème d'unification
de
*).
Miller montre aussi que le problème d'unification
de  Prolog peut être codé en un programme
Prolog peut être codé en un programme  et
que tout programme
et
que tout programme  Prolog peut être transformé en un
programme de ce fragment [Miller 91d].
Prolog peut être transformé en un
programme de ce fragment [Miller 91d].
La première implémentation de  Prolog date de 1987,
mais n'est pas complète
et absolument pas efficace
(
Prolog date de 1987,
mais n'est pas complète
et absolument pas efficace
(
 *).
Elle n'implémente pas tout le language,
en particulier pas les implications dans les buts.
La première implémentation complète date de 1991
(
*).
Elle n'implémente pas tout le language,
en particulier pas les implications dans les buts.
La première implémentation complète date de 1991
(
 *).
C'est un interpréteur écrit en Common Lisp.
Cette implémentation est suivie de près par le premier compilateur de
*).
C'est un interpréteur écrit en Common Lisp.
Cette implémentation est suivie de près par le premier compilateur de  Prolog
(
Prolog
(
 *).
C'est la première implémentation efficace en temps et en mémoire.
En 1996,
un nouvel interpréteur
(
*).
C'est la première implémentation efficace en temps et en mémoire.
En 1996,
un nouvel interpréteur
( Terzo*)
est diffusé.
Il résulte du portage de l'interpréteur
Terzo*)
est diffusé.
Il résulte du portage de l'interpréteur
 en Standard
en Standard  ,
et n'est pas plus efficace que l'original.
,
et n'est pas plus efficace que l'original.
Le typage,
et en particulier le polymorphisme,
est une dimension mal spécifiée des premiers développements
de  Prolog.
Les disciplines de typage varient et sont essentiellement monomorphes,
alors que le language concret et polymorphe.
En 1992,
Nadathur et Pfenning [Nadathur et Pfenning 92] propose une discipline de type
qui est incompatible avec la condition de tête*.
Le système
Prolog.
Les disciplines de typage varient et sont essentiellement monomorphes,
alors que le language concret et polymorphe.
En 1992,
Nadathur et Pfenning [Nadathur et Pfenning 92] propose une discipline de type
qui est incompatible avec la condition de tête*.
Le système  de Brisset et Ridoux,
dont la première diffusion date de 1991,
implémente la condition de tête.
En 1996,
Louvet et Ridoux propose une discipline fondée sur les types de deuxième ordre
(voir la section
«Typage polymorphe paramétrique»*).
de Brisset et Ridoux,
dont la première diffusion date de 1991,
implémente la condition de tête.
En 1996,
Louvet et Ridoux propose une discipline fondée sur les types de deuxième ordre
(voir la section
«Typage polymorphe paramétrique»*).

 Prolog (induction structurelle en).
n.f.
(rel. induction structurelle*)
Voir d'abord
induction structurelle en Prolog typé*.
L'induction structurelle en
Prolog (induction structurelle en).
n.f.
(rel. induction structurelle*)
Voir d'abord
induction structurelle en Prolog typé*.
L'induction structurelle en
 Prolog est un peu plus compliquée qu'au premier ordre
car un sous-terme d'un type donné n'est pas nécessairement construit
à l'aide des constructeurs de ce type :
il peut être construit à l'aide d'une
Prolog est un peu plus compliquée qu'au premier ordre
car un sous-terme d'un type donné n'est pas nécessairement construit
à l'aide des constructeurs de ce type :
il peut être construit à l'aide d'une
 -variable*.
Cela ne pose pas de problème si les occurrences de
-variable*.
Cela ne pose pas de problème si les occurrences de  -variables
ne sont pas du type de l'argument de l'induction structurelle,
et c'est précisément ce qui est assuré quand un type est
inductif*.
-variables
ne sont pas du type de l'argument de l'induction structurelle,
et c'est précisément ce qui est assuré quand un type est
inductif*.
Dans ce cas,
la relation à définir sur un type inductif l'est par des règles de la forme
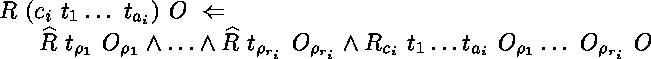
où 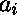 est l'arité de
est l'arité de 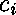 ,
,
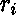 est le nombre d'arguments de
est le nombre d'arguments de 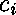 qui sont de type
qui sont de type 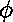 ou
ou
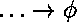 ,
les
,
les 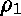 , ...,
, ..., 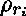 sont leurs rangs,
sont leurs rangs,
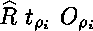 est
est
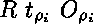 si
si 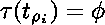 et
et 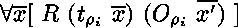 sinon,
où les
sinon,
où les 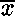 correspondent en nombre et en type aux arguments attendus
par
correspondent en nombre et en type aux arguments attendus
par 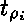 et les
et les 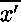 constituent un sous-ensemble des
constituent un sous-ensemble des 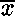 correspondant au type du second paramètre (le «résultat»)
de la relation à définir.
correspondant au type du second paramètre (le «résultat»)
de la relation à définir.
Par exemple,
étant donné le type des formules*
du calcul des prédicats du premier ordre,
la relation qui associe à une formule sa négation est définie par
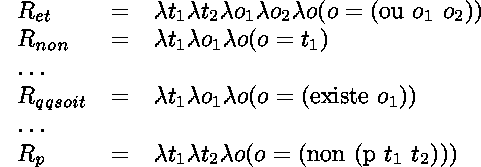
On voit ici (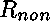 )
l'intérêt de passer à la relation
)
l'intérêt de passer à la relation 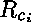 l'image par la relation
à définir des arguments du constructeur,
et les arguments eux-mêmes.
Cela évite des difficultés dont l'exemple type est que le calcul du car
d'une liste est beaucoup plus facile à réaliser inductivement que le calcul
du cdr [Pierce et al. 89].
l'image par la relation
à définir des arguments du constructeur,
et les arguments eux-mêmes.
Cela évite des difficultés dont l'exemple type est que le calcul du car
d'une liste est beaucoup plus facile à réaliser inductivement que le calcul
du cdr [Pierce et al. 89].
Pour un langage de programmation fonctionnel,
il est difficile de concevoir une induction structurelle sur des types
non-inductifs.
Cependant,
l'implication de
 Prolog permet de les traiter.
Prolog permet de les traiter.
Quand un type n'est pas inductif,
il peut y avoir des sous-termes arguments qui ont le type considéré,
mais ne sont pas construits à l'aide d'un des constructeurs du type.
Les variables universelles introduites dans les
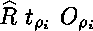 doivent alors être considérées comme des constructeurs du type considéré
qui sont introduits «à la volée» par la quantification universelle,
au lieu de l'être par une déclaration.
Chaque occurrence négative* de
doivent alors être considérées comme des constructeurs du type considéré
qui sont introduits «à la volée» par la quantification universelle,
au lieu de l'être par une déclaration.
Chaque occurrence négative* de 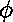 dans un des arguments
d'un de ses constructeurs est donc considérée comme une famille de
constructeurs de
dans un des arguments
d'un de ses constructeurs est donc considérée comme une famille de
constructeurs de 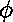 .
On lui associe donc une relation qui comporte tous les
paramètres des
.
On lui associe donc une relation qui comporte tous les
paramètres des 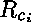 plus un autre qui permet
de capturer le contexte de la création d'un constructeur d'une famille.
Le contexte est aussi passé à la
relation associée au constructeur qui introduit l'occurrence négative.
Le schéma général devient alors
plus un autre qui permet
de capturer le contexte de la création d'un constructeur d'une famille.
Le contexte est aussi passé à la
relation associée au constructeur qui introduit l'occurrence négative.
Le schéma général devient alors
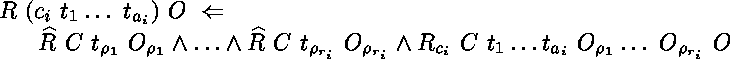
où 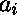 est l'arité de
est l'arité de 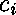 ,
,
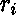 est le nombre d'arguments de
est le nombre d'arguments de 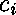 qui sont de type
qui sont de type 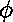 ou
ou
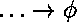 ,
les
,
les 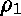 , ...,
, ..., 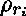 sont leurs rangs
et
sont leurs rangs
et
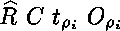 est
soit
est
soit 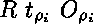 si
si 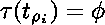 ,
soit
,
soit 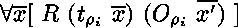 si
si 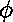 n'a pas d'occurrence négative,
ou
n'a pas d'occurrence négative,
ou
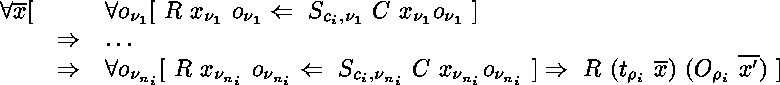
sinon,
où 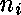 est le nombre d'occurrences négatives,
les
est le nombre d'occurrences négatives,
les 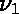 , ...,
, ..., 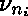 sont leurs rangs,
sont leurs rangs,
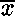 dénote
dénote 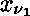 , ...
, ...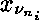 et
et
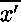 dénote un sous-ensemble de
dénote un sous-ensemble de 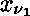 , ...
, ...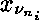 .
.
Par exemple,
étant donné le type l_terme*
des  -termes purs de niveau objet,
la relation de bon typage est définie par
-termes purs de niveau objet,
la relation de bon typage est définie par
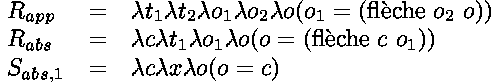
qui détermine le prédicat
r (app T1 t2) O :- r T1 O1 , r T2 O2 , O1 = (flèche O2 O) .
r (abs T1) O :-
pi x ( pi Ox
( pi Ox ( r x Ox :- Ox = C ) => r (T1 x) O1 ) ,
O = (flèche C O1) .
( r x Ox :- Ox = C ) => r (T1 x) O1 ) ,
O = (flèche C O1) .
qui se simplifie en le prédicat bien_typé*.
De la même façon,
la relation entre un  -terme et l'arbre de
de Bruijn* qui lui correspond est définie par
-terme et l'arbre de
de Bruijn* qui lui correspond est définie par
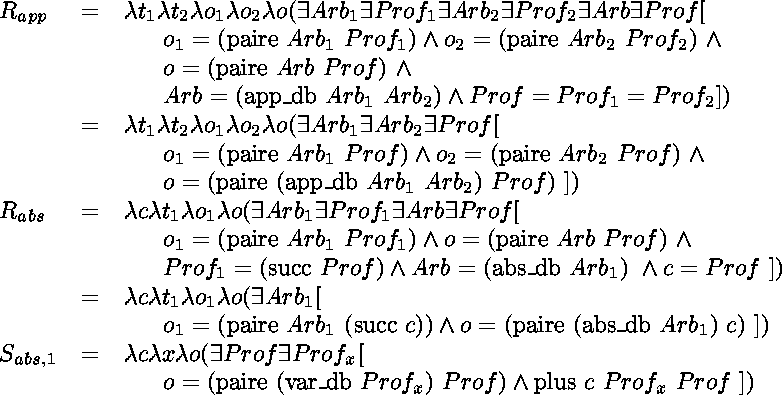
Il a fallu «empaqueter» dans une paire le résultat proprement dit
et un paramètre qui indique la profondeur courante
(le nombre de  -abstractions traversées, voir
-abstractions traversées, voir 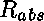 ).
C'est ce paramètre qui permet de calculer la distance qui sépare une
occurrence de variable de la
).
C'est ce paramètre qui permet de calculer la distance qui sépare une
occurrence de variable de la  -abstraction qui la lie
(
-abstraction qui la lie
(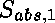 ).
Ces relations déterminent le prédicat
).
Ces relations déterminent le prédicat
de_bruijn (app T1 T2) O :-
de_bruijn T1 O1 , de_bruijn T2 O2 ,
sigma Arb1 (sigma Arb2
(sigma Arb2 (sigma Prof
(sigma Prof (
(
O1 = (paire Arb1 Prof) , O2 = (paire Arb2 Prof) ,
O = (paire (app_db Arb1 Arb2) Prof) ))) .
de_bruijn (abs T1) O :-
pi x (
(
pi Ox ( de_bruijn x Ox :-
( de_bruijn x Ox :-
sigma Prof (sigma Profx
(sigma Profx (
Ox = (paire (var_db Profx) Prof) ,
plus C Profx Prof )) )
(
Ox = (paire (var_db Profx) Prof) ,
plus C Profx Prof )) )
=> de_bruijn (T1 x) O1 ) ,
sigma Arb1 ( O1 = (paire Arb1 (succ C)) , O = (paire (abs_db Arb1) C) ) .
( O1 = (paire Arb1 (succ C)) , O = (paire (abs_db Arb1) C) ) .
qui se simplifie en
de_bruijn (app T1 T2) (app_db Arb1 Arb2) Prof :-
de_bruijn T1 Arb1 Prof , de_bruijn T2 Arb2 Prof .
de_bruijn (abs T1) (abs_db Arb1) C :-
pi x ( pi Prof
( pi Prof (pi Profx
(pi Profx ( de_bruijn x (var_db Profx) Prof :- plus C Profx Prof ))
( de_bruijn x (var_db Profx) Prof :- plus C Profx Prof ))
=> de_bruijn (T1 x) Arb1 (succ C) ) .
en remplaçant l'argument paire par deux arguments.

 Prolog (méta-interpréteur complet pour).
n.m.
(rel. vanilla interpreter*)
On peut enrichir le méta-interpréteur de base pour
Prolog (méta-interpréteur complet pour).
n.m.
(rel. vanilla interpreter*)
On peut enrichir le méta-interpréteur de base pour  Prolog
en lui ajoutant des paramètres de contrôle de la profondeur de la preuve,
afin qu'il termine toujours.
Prolog
en lui ajoutant des paramètres de contrôle de la profondeur de la preuve,
afin qu'il termine toujours.
% bd_i : Bounded Depth Interpreter
type bd_i o -> int -> int -> int -> o .
bd_i _ ProfMax _ ProfMax :- ! ,
fail .
bd_i true ProfAv ProfAv ProfMax :- ! .
bd_i (B1 , B2) ProfAv ProfAp ProfMax :- ! , % 
bd_i B1 ProfAv ProfInt ProfMax , bd_i B2 ProfInt ProfAp ProfMax .
bd_i (sigma B) ProfAv ProfAp ProfMax :- ! , % 
bd_i (B _) ProfAv ProfAp ProfMax .
bd_i (pi B) ProfAv ProfAp ProfMax :- ! , % 
pi c ( bd_i (B c) ProfAv ProfAp ProfMax ) .
( bd_i (B c) ProfAv ProfAp ProfMax ) .
bd_i (H => B) ProfAv ProfAp ProfMax :- ! , % 
( pi B (pi C
(pi C ( clause B C :- instance B H C )) => bd_i B ProfAv ProfAp ProfMax ) .
( clause B C :- instance B H C )) => bd_i B ProfAv ProfAp ProfMax ) .
% ( prédicat instance*)
prédicat instance*)
bd_i B ProfAv ProfAp ProfMax :-
clause B C , bd_i C (ProfAv+1) ProfAp ProfMax . %  et
et 
Ce méta-interpréteur explore l'arbre de recherche des preuves uniformes
jusqu'à une profondeur donnée,
ProfMax ;
il est donc incomplet.
Un contrôleur doit le lancer successivement jusqu'à
des profondeurs limites croissantes pour obtenir un méta-interpréteur complet.
% ibd_i : Iterative Bounded Depth Interpreter
type ibd_i o -> int -> int -> o .
ibd_i But ProfMax ProfMaxAv :-
bd_i But (0+1) ProfAtteinte ProfMax , ProfAtteinte 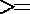 ProfMaxAv .
ProfMaxAv .
ibd_i But ProfMax _ :- ibd_i (ProfMax+1) ProfMax .
Le rôle du paramètre ProfMaxAv
et du test ProfAtteinte 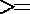 ProfMaxAv
est de filtrer les solutions produites à des
profondeurs déjà explorées.
Ce contrôleur peut être lancé de la façon suivante :
ProfMaxAv
est de filtrer les solutions produites à des
profondeurs déjà explorées.
Ce contrôleur peut être lancé de la façon suivante :
type prouve o -> o .
prouve But :- ibd_i But (0+1) 0 .

 Prolog (reconstruction pragmatique de).
n.f.
[Belleannée et al. 95, Ridoux 95]
Justification de la présence en
Prolog (reconstruction pragmatique de).
n.f.
[Belleannée et al. 95, Ridoux 95]
Justification de la présence en  Prolog de tous ses nouveaux dispositifs.
La reconstruction montre que si le premier pas est
l'introduction de la syntaxe des
Prolog de tous ses nouveaux dispositifs.
La reconstruction montre que si le premier pas est
l'introduction de la syntaxe des
 -termes et de la
-termes et de la  -équivalence en Prolog,
une analyse plus détaillée invite à ajouter tous les autres
dispositifs.
Le schéma suivant résume les relations de nécessité
entre les différentes composantes propres de
-équivalence en Prolog,
une analyse plus détaillée invite à ajouter tous les autres
dispositifs.
Le schéma suivant résume les relations de nécessité
entre les différentes composantes propres de  Prolog.
Les flèches se lisent «a besoin de».
Prolog.
Les flèches se lisent «a besoin de».
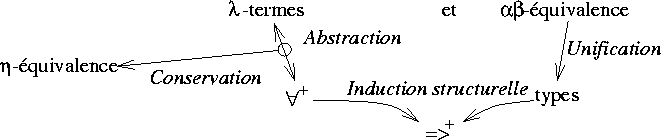
Une première considération est que pour maintenir la faisabilité de
l'unification il faut restreindre le domaine des
 -termes ;
le typage en est un moyen.
Une seconde considération est que pour permettre d'énoncer des
relations entre les abstractions des
-termes ;
le typage en est un moyen.
Une seconde considération est que pour permettre d'énoncer des
relations entre les abstractions des  -termes et leur corps,
il faut aussi introduire la
-termes et leur corps,
il faut aussi introduire la  -équivalence
et permettre des quantifications universelles dans les buts.
Enfin,
on doit introduire l'implication dans les buts pour faire cohabiter
programmation par induction structurelle et quantification universelle.
-équivalence
et permettre des quantifications universelles dans les buts.
Enfin,
on doit introduire l'implication dans les buts pour faire cohabiter
programmation par induction structurelle et quantification universelle.

 Prolog (sémantique de).
n.f.
On utilise habituellement la théorie de la démonstration pour
donner la sémantique de
Prolog (sémantique de).
n.f.
On utilise habituellement la théorie de la démonstration pour
donner la sémantique de  Prolog [Miller et al. 91]
au lieu de la théorie des modèles comme pour
Prolog [Lloyd 88].
Cela ne signifie pas qu'il n'y a pas de théorie des modèles pour ces formules.
Seulement,
elle ne désigne pas un modèle préférentiel aussi simple
que le plus petit modèle de Herbrand pour les clauses de Horn.
Le résultat principal est qu'une classe de démonstrations dirigées par le but,
celle des preuves uniformes*,
est complète par rapport à la prouvabilité intuitionniste pour
les formules héréditaires de Harrop.
Autrement dit,
toutes les formules héréditaires de Harrop
qui sont des théorèmes intuitionnistes ont une preuve uniforme.
Ou encore,
ne considérer que des preuves uniformes élimine des preuves,
mais pas de théorèmes intuitionnistes parmi les formules héréditaires de Harrop.
Prolog [Miller et al. 91]
au lieu de la théorie des modèles comme pour
Prolog [Lloyd 88].
Cela ne signifie pas qu'il n'y a pas de théorie des modèles pour ces formules.
Seulement,
elle ne désigne pas un modèle préférentiel aussi simple
que le plus petit modèle de Herbrand pour les clauses de Horn.
Le résultat principal est qu'une classe de démonstrations dirigées par le but,
celle des preuves uniformes*,
est complète par rapport à la prouvabilité intuitionniste pour
les formules héréditaires de Harrop.
Autrement dit,
toutes les formules héréditaires de Harrop
qui sont des théorèmes intuitionnistes ont une preuve uniforme.
Ou encore,
ne considérer que des preuves uniformes élimine des preuves,
mais pas de théorèmes intuitionnistes parmi les formules héréditaires de Harrop.
Les règles de déduction des connecteurs  ,
,  et
et  sont les suivantes :
sont les suivantes :
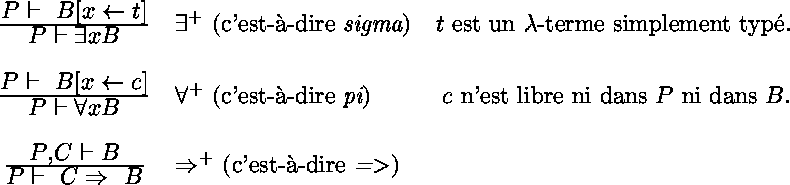
Ce sont des règles d'introduction à droite ;
leur connecteur d'intérêt est à droite du séquent conclusion
(c'est-à-dire dans le but).
La sémantique opérationnelle des mêmes connecteurs est la suivante :
-
Pour prouver un but
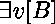 ,
il faut prouver le but
,
il faut prouver le but 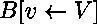 ,
où
,
où 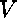 est une nouvelle variable logique ayant le type de
est une nouvelle variable logique ayant le type de 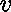 .
La variable
.
La variable 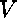 prendra une valeur
prendra une valeur  par unification.
par unification.
Contrairement à la règle de déduction qui suggère d'inventer
un  -terme
-terme  qui convient,
la règle opérationnelle reporte l'invention
de
qui convient,
la règle opérationnelle reporte l'invention
de  à la résolution ultérieure de problèmes d'unification.
Cela permet une invention de
à la résolution ultérieure de problèmes d'unification.
Cela permet une invention de  paresseuse et guidée par le besoin,
mais cela a aussi la conséquence que l'ordre d'invention des termes
n'est plus celui du développement de l'arbre de preuve partant de la
racine vers les feuilles.
paresseuse et guidée par le besoin,
mais cela a aussi la conséquence que l'ordre d'invention des termes
n'est plus celui du développement de l'arbre de preuve partant de la
racine vers les feuilles.
-
Pour prouver un but
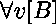 ,
il faut prouver le but
,
il faut prouver le but 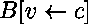 ,
où
,
où  est une nouvelle constante ayant le type de
est une nouvelle constante ayant le type de 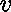 ,
sans que
,
sans que  n'entre dans les valeurs
de liaison de variables logiques plus anciennes.
n'entre dans les valeurs
de liaison de variables logiques plus anciennes.
La règle de déduction spécifie que  n'est libre ni dans le but ni dans le
programme.
Avec la règle opérationnelle pour
n'est libre ni dans le but ni dans le
programme.
Avec la règle opérationnelle pour  , il devient impossible
de vérifier cette condition au moment de l'utilisation de la règle pour
, il devient impossible
de vérifier cette condition au moment de l'utilisation de la règle pour
 .
En effet,
ni le but ni le programme ne sont complètement déterminés.
Il faut donc transformer la condition sur
.
En effet,
ni le but ni le programme ne sont complètement déterminés.
Il faut donc transformer la condition sur  en une contrainte sur les
variables logiques qui apparaissent dans le but et le programme :
on ne doit pas leur substituer de valeurs de liaison qui contiennent
en une contrainte sur les
variables logiques qui apparaissent dans le but et le programme :
on ne doit pas leur substituer de valeurs de liaison qui contiennent  .
C'est donc l'unification qui doit s'acquitter de cette vérification
(
.
C'est donc l'unification qui doit s'acquitter de cette vérification
( test d´occurrence*).
test d´occurrence*).
-
Pour prouver un but
 ,
il faut prouver le but
,
il faut prouver le but  dans le programme augmenté de
la clause
dans le programme augmenté de
la clause  .
La clause
.
La clause  ne reste dans le programme que pour la durée
de la preuve de
ne reste dans le programme que pour la durée
de la preuve de  .
Elle est supprimée dès que la preuve est terminée.
.
Elle est supprimée dès que la preuve est terminée.

 Prolog (termes de).
n.m.
Les termes de
Prolog (termes de).
n.m.
Les termes de  Prolog sont des
Prolog sont des
 -termes simplement typés*.
Les identificateurs de constante,
-termes simplement typés*.
Les identificateurs de constante,
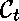 ,
sont déclarés en utilisant la directive
type.
Par exemple,
le programme conc contient les déclarations suivantes :
,
sont déclarés en utilisant la directive
type.
Par exemple,
le programme conc contient les déclarations suivantes :
type nil (list T) .
% 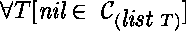
type '.' T -> (list T) -> (list T) .
% 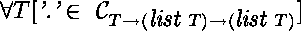
type conc (list T) -> (list T) -> (list T) -> o .
% 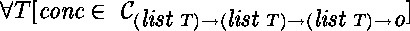
La déclaration de nil montre qu'il s'agit d'une constante
non-fonctionnelle.
La déclaration de «.» montre qu'il s'agit d'une fonction à deux
arguments.
Ces deux constantes permettent de
construire des listes polymorphes homogènes* :
listes polymorphes dont tous les éléments ont le même type.
Enfin,
le type résultat de conc, o,
montre que conc est un symbole prédicatif.

 Prolog (type de).
n.m.
Les types de
Prolog (type de).
n.m.
Les types de  Prolog sont des types simples*
augmentés de variables*
afin d'introduire du polymorphisme dans le système.
On suppose que le
Prolog sont des types simples*
augmentés de variables*
afin d'introduire du polymorphisme dans le système.
On suppose que le 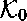 de la définition des
types simples contient toujours la constante o
pour le type des propositions.
Les identificateurs de constructeur de types,
de la définition des
types simples contient toujours la constante o
pour le type des propositions.
Les identificateurs de constructeur de types,
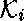 ,
sont déclarés en utilisant la directive kind :
par exemple,
,
sont déclarés en utilisant la directive kind :
par exemple,
kind o type . % 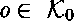
kind list type -> type . % 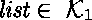
La déclaration de list montre qu'il s'agit d'un constructeur de type
qui doit être appliqué à un type pour former un autre type.
Ces deux déclarations sont standard dans un système  Prolog concret.
Prolog concret.

 Prolog.
(
Prolog.
( type paramétrique*)
type paramétrique*)

 .
Le système
.
Le système  est
l'implémentation de
est
l'implémentation de
 Prolog réalisée à l´
Prolog réalisée à l´ par Pascal Brisset et Olivier Ridoux
[Brisset et Ridoux 92b, Brisset et Ridoux 92a].
Il est distribué sous licence
par Pascal Brisset et Olivier Ridoux
[Brisset et Ridoux 92b, Brisset et Ridoux 92a].
Il est distribué sous licence  (Free Software Foundation).
(Free Software Foundation).
Le système  est construit autour d'un compilateur de
est construit autour d'un compilateur de
 Prolog vers C.
Il implémente tout
Prolog vers C.
Il implémente tout  Prolog
et permet la connexion avec C :
appel de C depuis
Prolog
et permet la connexion avec C :
appel de C depuis  Prolog, ou de
Prolog, ou de  Prolog depuis C,
la procédure principale pouvant être en C ou en
Prolog depuis C,
la procédure principale pouvant être en C ou en  Prolog.
Il implémente la condition de tête*,
quelques dispositifs communément offerts dans les systèmes Prolog
(par exemple, freeze)
et d'autres moins communs
(par exemple,
la capture des continuations*).
Il offre aussi un environnement de trace et des capacités de mesure de
l'utilisation des prédicats d'une application.
Prolog.
Il implémente la condition de tête*,
quelques dispositifs communément offerts dans les systèmes Prolog
(par exemple, freeze)
et d'autres moins communs
(par exemple,
la capture des continuations*).
Il offre aussi un environnement de trace et des capacités de mesure de
l'utilisation des prédicats d'une application.
Le système  est implémenté au dessus d'une version logicielle de
est implémenté au dessus d'une version logicielle de
 *.
Cela forme un environnement d'exécution avec lequel les programmes utilisateurs
sont reliés lors de leur compilation.
*.
Cela forme un environnement d'exécution avec lequel les programmes utilisateurs
sont reliés lors de leur compilation.
Voir aussi la section «Un système ouvert»*.




Next: Q
Up: A-Z
Previous: O
Olivier Ridoux
Mon Apr 27 11:10:23 MET DST 1998
 Partage de représentation.
n.m.
Désigne le fait de reconnaître que des objets d'origines distinctes
sont équivalents,
et de les faire partager une représentation commune.
C'est un complément indispensable du ramasse-miette pour
obtenir une gestion de mémoire efficace.
En
Partage de représentation.
n.m.
Désigne le fait de reconnaître que des objets d'origines distinctes
sont équivalents,
et de les faire partager une représentation commune.
C'est un complément indispensable du ramasse-miette pour
obtenir une gestion de mémoire efficace.
En