Best viewed in 24pt and full-screen

T

type hanoi int -> string -> string -> string -> ((list mv) -> (list mv)) -> o .
dynamic hanoi .
hanoi 1 A _B C z[(mouvement A C)|z] .
hanoi N A B C z(M1 (M2 (M3 z))) :- N > 1 , N1 is N-1 ,
      hanoi N1 A C B M1 , hanoi 1 A B C M2 , hanoi N1 B A C M3 .

type tours_hanoi_memo int -> int -> string -> string -> string -> ((list mv) -> (list mv)) -> o .
tours_hanoi_memo I N A B C M :- I < N , I1 is I+1 ,
      pi a(pi b(pi c( hanoi I a b c (MI a b c) , ! ))) ,
      ( pi A(pi B(pi C( hanoi I A B C (MI A B C) ))) => tours_hanoi_memo I1 N A B C M ) .
tours_hanoi_memo N N A B C M :- hanoi N A B C M .

Résolution du problème des tours de Hanoi par mémoïsation. Elle est faite à l´aide de l´implication, sans modifier le programme naïf (hanoi). Appeler (tours_hanoi_memo 1 NbDisques "1" "2" "3" Mouvements).

-Terme. n.m. ( ex.progr. déclaration l_terme*) Terme du -calcul* construit avec la -abstraction*, l´application* et éventuellement un jeu de constantes.

Terme rationnel. n.m. Terme éventuellement infini et composé d'un nombre fini de sous-termes différents. Un terme fini (par exemple, un terme de l´univers de Herbrand*) est évidemment rationnel. Dans la figure suivante, le terme de gauche, qui représente essentiellement la liste des entiers, n'est pas rationnel, tandis que celui du milieu l'est. Il représente essentiellement une liste de 0 et de 1 alternés.

 

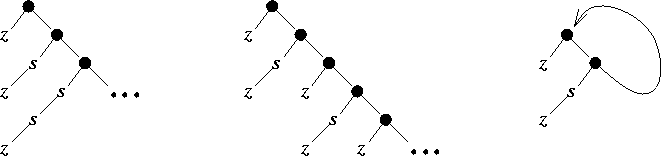
Un terme rationnel, même infini, peut être représenté finiment par un graphe dont les sommets sont les sous-termes différents qui le composent et les arcs représentent la relation de sous-terme. Dans la figure ci-dessus, le graphe de droite est la représentation finie du terme du milieu.

L´unification* des termes rationnels est unitaire, décidable et même relativement aisée [Huet 76]. L'unification mise en uvre pratiquement dans les systèmes Prolog est incorrecte à cause de l'omission du test d´occurrence*. Remplacer les termes de Prolog par des termes rationnels est une réponse à ce problème.

-Terme simplement typé. n.m. ( ex.progr. déclaration l_terme_st*) Les -termes simplement typés sont engendrés par la grammaire suivante :

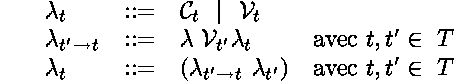
La grammaire est essentiellement la même que celle des -termes non-typés, mais les non-terminaux sont ici décorés d'attributs qui sont des types. L'accord en type doit être vérifié lors de toute dérivation utilisant cette grammaire. Les  et  sont respectivement des identificateurs de constantes et de variables dont le type est .

Terzo. Dernière en date (1997) des implémentations de Prolog. C'est un interpréteur écrit en Standard . C'est un travail commencé par Frank Pfenning et Conal Eliott à l'université de Carnegie Mellon, poursuivi par Amy Felty au laboratoire Bell Labs de , et finalisé par Philip Wickline à l'université de Pennsylvanie (UPenn).

Test d´occurrence. n.m. Test préalable à la formation d'une substitution par lequel on vérifie que  et  sont compatibles. En Prolog, ce test consiste à vérifier que  n'a pas d'occurrence dans .

Le test d'occurrence s'interprète logiquement en termes d´élimination de quantificateurs*. En effet, dans une formule , la variable  peut dépendre de , mais pas dans une formule . Par exemple, on prouve en prenant  égal à , mais on n'a pas le droit de prouver de cette façon. La dépendance peut être indirecte comme dans où  semble pouvoir dépendre de , mais ne le peut pas car il est en fait synonyme de  qui ne peut pas dépendre de .

Une des manières qu'a l'élimination des quantificateurs de représenter les dépendances entre variables est de remplacer les variables essentiellement universelles par des termes dans lesquelles figurent les variables essentiellement existentielles qui ne peuvent pas en dépendre (c'est-à-dire celles qui sont quantifiées plus à gauche). C'est la skolémisation*. Une autre manière est de remplacer les variables existentielles par des applications de fonctions inconnues aux variables universelles dont elles peuvent dépendre (c'est-à-dire celles qui sont quantifiées plus à gauche). C'est l´antiskolémisation*.

En Prolog, tout se passe comme si l'élimination des quantificateurs existentiels etait faite statiquement par skolémisation en utilisant la première manière. En Prolog, les possibilités d'imbrications des quantifications sont plus variées et les deux manières sont utilisées : la première, statiquement, pour ce qui est compatible avec Prolog et la deuxième, dynamiquement, pour les quantifications de Prolog qui ne sont pas réductibles à celles de Prolog. Dans le dernier cas, on n'énumère pas vraiment les variables universelles dont une variable existentielle peut dépendre. On numérote les variables universelles par ordre d'imbrication de leurs quantifications et on ne note que le plus grand des numéros des variables universelles dont elle peut dépendre.

En Prolog, le test d'occurrence préalable à la substitution consiste donc à vérifier que  et aucune variable universelle interdite dans  n'ont d'occurrence rigide* dans , et à propager dans les variables existentielles de  les variables universelles interdites de . Par exemple, la recherche d'une preuve de se déroule comme suit, où on note pour chaque variable existentielle les variables universelles dont elle peut dépendre. Ainsi, dénote que  peut dépendre de  et de , et que donc toutes les autres variables universelles sont interdites.

Le but : .

Élimination de . Reste .

Élimination de . Reste .

Élimination de . Reste .

Substitution où le test d'occurrence propage les interdits de  à . Reste .

Échec dû à un test d'occurrence négatif : ne peut pas dépendre de .

Dans le cas où le terme  a une occurrence flexible*, soit de la variable , soit de variables universelles interdites dans , il faut que l'une des occurrences flexibles sur le chemin qui y mène soit remplacée par un terme qui «coupe» le chemin. Par exemple, la recherche d'une preuve de se déroule comme suit. Ici, et , et et , sont des constantes et des variables d'un environnement visible de la formule. On ne connaît pas les relations qu'entretiennent , , et .

Le but : .

Élimination de . Reste .

Élimination de . Reste .

Substitution  .

Dans cet exemple, le test d'occurrence détecte un chemin flexible vers l'occurrence interdite . Ce chemin devra être coupé soit en , , soit en , , soit aux deux applications flexibles. Comme il n'est pas facile de gérer une disjonction de substitutions, le système * suspend la résolution du problème d'unification comme il est souvent fait en programmation logique avec contraintes. La résolution du problème sera reprise quand soit  soit  se sera précisée.

En général, les systèmes Prolog n'implémentent pas le test d'occurrence, ou alors il n'est actif qu'à la demande. Cela fait de ces systèmes des démonstrateurs incorrects en toute généralité, mais on observe que le test d'occurrence est le plus souvent inutile, et on connaît assez bien les situations où on peut prouver qu'il l'est [Deransart et al. 91].

Inversement, on observe qu'en Prolog la partie du test d'occurrence qui est spécifique (propagation des variables universelles interdites) est le plus souvent utile car elle conditionne la bonne formation des -abstractions*. C'est lié à la notion de variables essentiellement universelles* qui fait correspondre variables universelles et -variables*. La partie commune avec Prolog reste le plus souvent inutile, mais la formalisation des conditions de son inutilité n'a pas encore été faite.

Une solution pour affranchir Prolog du test d'occurrence est de changer son domaine de calcul. Si on remplace les termes de Prolog par des termes rationnels* comme en Prolog  ( Colmerauer*), il est assez facile de réaliser une implémentation pour laquelle l'unification n'est pas plus coûteuse que l'unification de Prolog sans test d'occurrence [Le Huitouze 88]. On ne peut pas suivre cette approche en Prolog car cela fait perdre la propriété de normalisation forte*. En effet, on peut très facilement représenter un combinateur de point-fixe avec un -terme rationnel, même s'il est simplement typé. Le -terme rationnel Y' suivant est un combinateur de point fixe.

 

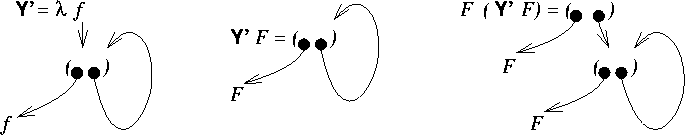
Il est facile de constater que (F ( Y' F)) est égal à ( Y' F) modulo l'égalité des termes rationnels. Le -terme rationnel Y' se comporte donc comme un combinateur de point-fixe.

. Une opération élémentaire ajoutée au semi-algorithme de Huet* dans son implémentation.

Une paire flexible-rigide* n'est pas passée directement à la procédure *, non plus qu'une paire flexible-flexible n'est automatiquement suspendue. Une telle paire est d'abord passée à la procédure , qui essaie de la résoudre en appliquant des heuristiques «simples». Si aucune heuristique ne s'applique, la paire est alors passée à  ou suspendue.

Les heuristiques reconnaissent des paires (dites «paires triviales») sous des formes diverses. Si une telle paire est reconnue et si la variable  n'apparaît pas dans le terme , alors la substitution est un unificateur de cette paire. Le test d´occurrence* est plus compliqué que son homologue du premier ordre car les occurrences de  dans  ne causent pas toutes un échec. Il se complique encore avec l'introduction des quantifications.

Une bonne procédure doit reconnaître une paire triviale sous les formes suivantes.

• La paire , où est une permutation de , est -équivalente à une paire triviale, à une permutation près. Dans ce cas, la substitution solution est
• La paire , où est une permutation de toutes les variables universelles de portée entre et , est équivalente, par antiskolémisation*, à pour une nouvelle variable logique  de portée . Dans ce cas, la substitution solution est où les substitutions sont notées explicitement* dans la valeur de liaison. C'est un cas très fréquent parce que la programmation en Prolog revient souvent à échanger des variables universelles et des -variables (c'est-à-dire des variables essentiellement universelles* au niveau des formules et des variables essentiellement universelles au niveau des termes).

Type abstrait. n.m. Les quantifications de Prolog fournissent un support naturel pour définir des types abstraits et leurs méthodes [Miller 89a]. L'idée est d'exploiter l'identité suivante :

Cette identité montre qu'en Prolog on peut aussi avoir des quantifications existentielles au niveau des clauses, mais à la condition qu'elles soient complètement extérieures à une clause, car alors on pourra les remplacer par des quantifications universelles au niveau d'un but. D'après les règles d'élimination des quantificateurs, ces quantifications existentielles seront éliminées en remplaçant les variables quantifiées par de nouvelles constantes. Par définition, ces constantes ne peuvent pas être connues du programmeur. On peut donc les considérer comme des constructeurs cachés d'un type abstrait dont les méthodes sont les prédicats laissés visibles. Par exemple, les déclarations et définitions suivantes,

kind pile type -> type .

type est_vide (pile A) -> o .

type sommet A -> (pile A) -> (pile A) .

type hauteur (pile A) -> int -> o .

sigma vide(sigma empiler(

      est_vide vide ,

      pi S(pi P( sommet S P (empiler S P) )) ,

      hauteur vide zéro ,

      pi S(pi P(pi H( hauteur (empiler S P) (succ H) :- hauteur P H ))) )) .

introduisent un type abstrait pile, dont les constructeurs vide et empiler sont cachés, mais dont les méthodes est_vide, sommet et hauteur sont visibles.

Type inductif. n.m. Se dit du type d'une structure de données dont les constructeurs n'ont des sous-termes de ce type dans leurs arguments qu'en des occurrences positives [Böhm et Berarducci 85, Pierce et al. 89]. Il faut se rappeler que selon la correspondance de Curry-Howard* la flèche des types simples est l'analogue de l'implication du calcul des propositions. Comme elle, elle introduit une notion d'occurrences négatives* et positives* selon la définition suivante :

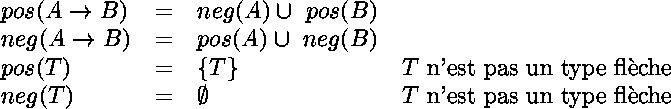
Par exemple, pour un type  égal à , on a et .

En Prolog, la notion de type inductif permet de décider sans avoir recours au raisonnement opérationnel s'il faut utiliser l'implication dans les buts dans une induction structurelle ( induction structurelle en Prolog*). Si le type d'une structure de données est inductif alors on en déduit facilement une fonction d'induction structurelle sur ses constructeurs [Böhm et Berarducci 85, Pierce et al. 89], sans utiliser l'implication. En revanche, si le type n'est pas inductif, l'induction structurelle standard ne suffit pas. Dans tous les cas (inductif ou non), la quantification universelle dans les buts sera nécessaire pour les arguments d'ordre supérieur. De plus, dans le cas non-inductif, l'implication dans les buts sera aussi nécessaire pour les occurrences négatives.

Les occurrences négatives correspondent aux types des variables universelles utilisées pour interpréter les abstractions. Donc, si le type d'intérêt a une occurrence négative, il faudra utiliser l'implication pour augmenter le programme afin de prendre en compte la constante universelle utilisée pour interpréter la quantification universelle.

L'exemple d'induction structurelle sur les formules ( prédicat norm_nég*) n'utilise pas l'implication. C'est parce que le type formule* est inductif. Ses constructeurs sont soit des connecteurs (et, etc.), soit des quantificateurs (qqsoit, etc.). Le type de tous les arguments de et est formule. Le type de l'unique argument de qqsoit est individuformule. Or, on a neg(formule)= et neg(individuformule)=individu. Aucun ne contient formule, donc le type formule est inductif.

Cette exemple montre aussi que les quantifications du métalangage sont utilisées pour interpréter la structure des formules objet, indépendamment de leur sémantique. Ici, la même quantification universelle est utilisée pour traiter les quantifications existentielles et les quantifications universelles des formules objet.

Au contraire, tous les exemples présentés sur les -termes objets ( prédicats bien_typé* et de_bruijn*) utilisent l'implication. Montrons que le type l_terme* n'est pas inductif. Ses constructeurs sont app et abs, et le type de abs est (l_termel_terme)l_terme. Le type de l'unique argument de abs est donc l_termel_terme. Or neg(l_termel_terme)=l_terme. Le type l_terme a une occurrence négative dans le type d'un argument d'un de ces constructeurs ; il n'est donc pas inductif.

Type oublié. n.m. Instance d'une variable de type qui est oubliée par un type oublieur*. Avec les types des variables logiques, ce sont les seuls types qu'il est nécessaire de représenter à l'exécution [Brisset et Ridoux 92b, Brisset et Ridoux 94].

Type oublieur. n.m. Type qui viole la condition de transparence*. Par exemple, tous les types de prédicats polymorphiques sont oublieurs.

Type paramétrique. n.m. [Louvet et Ridoux 96, Louvet 96] La discipline de typage du -calcul* polymorphique du second ordre, ( cube de Barendregt*), peut être transposée à la programmation logique. Cela permet de s'affranchir de la condition de tête* et de décrire convenablement la représentation des types à l'exécution. Le système obtenu en appliquant cette discipline à Prolog est appelé Prolog (voir la section «Typage polymorphe paramétrique»*).

Type produit. n.m. Un type produit est celui de «fonctions» dont le type du résultat, , peut dépendre de la valeur du paramètre, . Un type flèche peut être considéré comme une abréviation d'un type produit lorsque le type du résultat de dépend pas de la valeur du paramètre.

Pourquoi ce nom de «type produit» ? L'explication pour les fonctions d'un type fini  dans un autre type fini  est assez simple. Elles sont complètement déterminées par leurs graphes, qui sont des vecteurs de . On peut donc noter le type de ces fonctions par , et cette notation s'étend sans difficulté au cas où  n'est pas fini, et avec un peu plus de difficulté au cas où  ne l'est pas. Considérons maintenant des fonctions d'un type fini  dans des types finis  déterminés pour chaque élément de . Elles sont encore complètement déterminées par leurs graphes, qui sont des vecteurs de , qu'il est plus commode de noter . À nouveau cette notation s'étend au cas infini. Si tous les sont les mêmes, on retrouve naturellement la notation .

Si les sont des types, alors le type produit modélise la notion de polymorphisme paramétrique (voir la section «Typage polymorphe paramétrique»*). Cette faculté correspond à la face «non prédicative» (aussi notée ) du cube de Barendregt* ( figure 1*). Si les sont des termes, alors le type produit modélise la notion de type dépendant. Cette faculté correspond à la face des «preuves» (aussi notée ).

Type simple. n.m. Les types simples [Church 40, Barendregt 91] sont engendrés par la grammaire suivante :

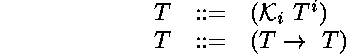
Les sont des identificateurs de constructeurs de type d'arité . La deuxième règle est la règle de formation des types de fonctions ; le type peut être interprété comme celui des fonctions de  vers . On admet que la flèche est associative à droite, ce qui rend certaines parenthèses inutiles : par exemple, ooo dénote le même type que (o(oo)). La notation concrète de  dans les programmes est ->.

La représentation en Prolog des types simples de niveau objet est la suivante :

kind type_simple type .

type flèche type_simple -> type_simple -> type_simple .

type base type_simple .

Les règles de bon typage au niveau objet sont les suivantes :

type bien_typé l_terme -> type_simple -> o .

bien_typé (app E F) Tau :- bien_typé E (flèche Sigma Tau) , bien_typé F Sigma .

bien_typé (abs E) (flèche Sigma Tau) :- pi x( bien_typé x Sigma => bien_typé (E x) Tau ) .