Best viewed in 24pt and full-screen

R

type renverser (list A) -> (list A) -> o .
renverser L R :-
         pi renv(   pi A(pi As(pi Rs(renv [A|As] Rs :- renv As [A|Rs])))
                      => renv [] R
                      => renv L [] ) .

Renversement de liste.

Radical. n.m. (syn. rédex*)

Rédex. n.m. Occurrence dans un terme où une règle de réduction peut s'appliquer.

-Rédex. n.m. ( ex.progr. prédicat beta_redex*) -terme de la forme . Ces termes sont candidats à être -réduit*.

-Rédex. n.m. ( ex.progr. prédicat beta_eta_redex*) Beaucoup de -expansions sont explicitement réalisées par le compilateur de * ou par l'unificateur. On peut donc marquer les -rédex de manière à reconnaître au moindre coût les cas d'application de l'axiome de -équivalence*. Cela procure un gain de complexité dans l'implémentation de Prolog (Voir la section «Le rôle de la -équivalence»*).

-Rédex. n.m. ( ex.progr. prédicat eta_redex*) -terme de la forme , où  n'a pas d'occurrence dans . Ces termes résultent d'une -expansion*. Reconnaître ces termes est important pour l'implémentation de la -réduction*. En effet, on peut spécialiser la règle de -réduction pour le cas où le terme qui joue le rôle de fonction est un -rédex ( -rédex*).

-Réduction. n.f. Action de réécrire un terme qui a la forme de la partie gauche de l'égalité qui définit la -équivalence* en un terme qui a la forme de la partie droite, toutes choses restant égales par ailleurs. C'est la principale règle de calcul du -calcul*. Elle peut être interprétée comme la substitution de paramètres effectifs à des paramètres formels.

Réduction de graphe. n.f. (rel. combinateurs*, -rédex* et partage de représentation*) Technique d'implémentation d'un système de réécriture où les termes sont représentés par le graphe de leur syntaxe abstraite et les occurrences d'une même variable sont représentées par un même nud. Les substitutions s'effectuent en ajoutant un arc entre la variable substituée et sa valeur de substitution. La réécriture d'un rédex s'effectue en effaçant les arcs issus du nud qui représente le rédex, en construisant le graphe de la forme réduite et en ajoutant un arc entre le premier et le second.

La réduction de graphe a de bonne qualité de gestion de mémoire : partage de représentation et simplicité d'implémentation. Il ne faut cependant pas l'implémenter naïvement. Elle peut être beaucoup améliorée en ajoutant au système de réécriture des règles redondantes qui tiennent compte des particularités des rédex. Dans le cas de l'implémentation de la -équivalence* pour Prolog, il est important de prendre en compte les combinateurs et les -rédex (voir les sections «Le rôle des combinateurs»* -- et «Le rôle de la -équivalence»*).

Réflexion. n.f. (rel. réification*) Action d'intégrer au niveau de l'interprétation d'un métaprogramme (ou d'un programme qui se comporte en partie comme tel) une structure de niveau objet. Une des formes les plus connues de réification/réflexion est la capture de continuation en Scheme. Les continuations* sont d'abord des structures abstraites qui permettent de donner la sémantique des programmes. Le langage Scheme donne le moyen de les capturer comme des termes ordinaires (réification), puis de les réinjecter dans l'interpréteur. Un dispositif similaire est offert par *. Il permet la capture de la continuation de succès (la résolvante*) et de la continuation d'échec (pile de recherche*) [Brisset et Ridoux 93].

Prolog offre une autre forme de réification/réflexion fondée sur la notion de quantification essentiellement universelle*. Là, une -abstraction* peut être réfléchie sur une quantification universelle*, et inversement, une quantification universelle peut être réifiée en une -abstraction.

Règle. n.f.

1) ( règle de déduction*)

2) (syn. clause*) S'emploie en référence aux domaines des systèmes experts ou des bases de données déductives.

Règle de déduction. n.f. Assemblage de formules qui spécifie que est vraie si , ...et le sont. On appelle prémisse la partie haute d'une règle de déduction et conclusion la partie basse. Un cas particulier intéressant est celui où les formules sont des séquents*.

Réification. n.f. (rel. réflexion*) Action de créer une représentation de niveau objet d'une structure d'un métaprogramme. On peut alors la modifier ou en calculer une variante et la réfléchir sur le métaprogramme pour en produire les effets.

Représentation close. n.f. Technique de métaprogrammation* où les variables objet* sont représentées par des constantes du métalangage. L'avantage est une distinction nette entre le métaprogramme et son objet. L'inconvénient est que la substitution d'un terme à une variable objet nécessite de copier tout le contexte de cette variable. C'est une opération coûteuse et délicate si on veut conserver les partages de représentation*.

Représentation non-close. n.f. Technique de métaprogrammation* où les variables objet* sont représentées par des variables du métalangage. L'avantage est que la substitution d'un terme à une variable objet est «gratuite» : c'est la substitution du métalangage. L'inconvénient est que la substitution du métalangage n'est pas forcément une implémentation correcte de celle du langage objet (par exemple, non-respect des portées*). Cela force à mettre en uvre des contrôles qu'il faut doser finement si on veut préserver l'avantage de cette représentation. C'est la représentation la plus souvent utilisée en Prolog*.

Représentation par abstraction. n.f. Technique de métaprogrammation* où les variables objet* sont représentées par des -variables*. L'avantage est que, pour une large classe d'application, la substitution d'un terme à une variable objet est celle du métalangage, et qu'elle respecte les portées.

Requête. n.f. (syn. question*) Formule soumise à un interpréteur de programmation logique* pour qu'il en cherche une preuve. On peut la considérer comme une clause* dont la tête* est vide ou le littéral* faux.

Beaucoup de systèmes Prolog donnent accès à l'interpréteur du langage via un superviseur. On peut alors émettre interactivement des requètes dont le résultat peut consister en un échec, ou en une substitution solution*. L'implémentation * de Prolog est compilée et n'offre pas de superviseur. Les questions sont aussi compilées.

Résolution. n.f. [Robinson 65] Règle de réfutation qui est complète pour le calcul des prédicat pour peu que la formule à réfuter soit en forme normale conjonctive*. On peut la considérer comme une généralisation du modus ponens, qui permet de déduire d'une implication et de son hypothèse sa conclusion.

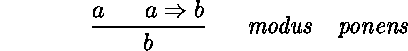
On peut augmenter le modus ponens pour tenir compte d'hypothèses et de conclusions multiples qui ne se superposent pas complètement. On obtient ainsi une règle qui ressemble à la règle de coupure*.

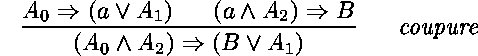
Si on convient que les formules atomiques* peuvent contenir des variables libres, il ne suffit pas de vérifier que les deux formules  des prémisses sont identiques. Il faut les comparer modulo la substitution de termes aux variables ( *). On obtient ainsi la règle de résolution.

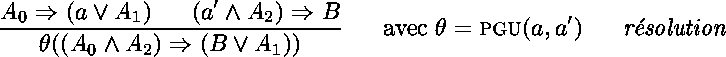
L'apport fondamental de la règle de résolution est qu'elle constitue à elle seule un système déductif complet, pour peu que la formule à démontrer soit sous forme normale conjonctive*, alors que le modus ponens n'est pas complet. Ici, on considère les clauses de la forme normale conjonctive comme les axiomes du système déductif.

Comme la mise sous forme normale conjonctive passe par une skolémisation*, et ne préserve donc que la réfutabilité, la méthode de preuve basée sur la résolution est une méthode par réfutation. Étant donnée une théorie  et une question , on applique donc la résolution à et le but* est la clause vide ().

On peut observer que si les prémisses sont des clauses de Horn* (c'est-à-dire  est vide et  est atomique) la conclusion l'est aussi. La résolution préserve donc la propriété d'être une clause de Horn.

Deux spécialisations de la règle de résolution décrivent deux stratégies d'évaluation de Prolog. Dans la stratégie remontante, la résolution de faits* et d'une clause du programme permet de déduire d'autres faits. Cette spécialisation revient à une forme de modus ponens.

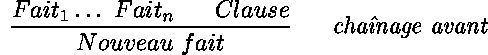
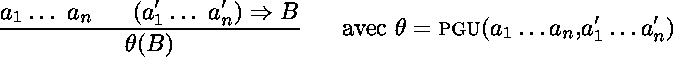
Dans la stratégie descendante, la résolution d'une question et d'une clause permet de déduire une autre question.

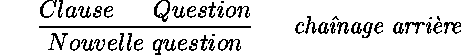
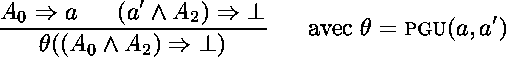
Résolvante. n.f. (rel. résolution*)

1) Disjonction de littéraux* obtenue par l'application du principe de résolution.

2) (En Prolog) (rel. continuation de succès*) Disjonction de littéraux* négatifs* qui est soit la requète initiale, soit obtenue par l'application du principe de résolution à une résolvante déjà obtenue et à une clause du programme. Dans ce sens, une résolvante est la continuation de succès. On la considère souvent comme la conjonction des buts* à résoudre.

3) (En Prolog, par analogie au cas de Prolog) (rel. continuation de succès*) Conjonction de formules de Harrop* positives* qui est soit la requète initiale, soit obtenue par l'application de règles de déduction à une résolvante déjà obtenue et à une clause du programme. Dans ce sens, une résolvante est aussi la continuation de succès.

En , la résolvante continuation de succès est représentée par une structure de données de * qui est construite progressivement et exploitée par les fonctions qui réalisent les prédicats Prolog. Ces fonctions sont générées par le compilateur. C'est une différence importante avec l'usage de la (voir la section «Étendre la »*) où la résolvante est en fait représentée par une pile d'appel de procédure. Dans la solution de , la résolvante est représentée dans la même technologie que les termes ; cela rend triviale la capture de continuation. Cette manière de faire réalise naturellement ce qui nécessite des opérations assez complexes avec la  [Noyé 94a, Noyé 94b] : optimisation de dernier appel (souvent appelée , pour tail récursion optimisation) et élagage d'environnement, (environment trimming).

Réversibilité. n.f. (rel. mode*) (ant. directionnalité*) Capacité des programmes logiques de ne pas toujours figer de dépendance fonctionnelle entre les arguments des relations. Par exemple, le prédicat suivant exprime la relation qu'entretiennent trois listes fonctionnelles* telles que la troisième est la concaténation des deux premières.

conc_f L_1 L_2 z(L_1 (L_2 z)) .

Ce même prédicat peut être utilisé pour réaliser la concaténation de deux listes L_1 et L_2, (conc_f L_1 L_2 Reponse), supprimer un préfixe P d'une liste L, (conc_f P Reponse L), supprimer un suffixe S, (conc_f Reponse S L), ou scinder non-déterministement une liste L en deux parties, (conc_f Partie_1 Partie_2 L).

Le principal avantage est de permettre d'écrire un seul programme au lieu de plusieurs (3 pour conc_f), et donc d'éviter des incohérences. Il est particulièrement important que les prédicats de bibliothèque soient les plus réversibles possibles. Cela rend leur emploi plus simple et plus sûr même lorsque le programme utilisateur est complètement orienté. Il subsiste alors un problème d'implémentation : faire que l'utilisation directionnelle d'un prédicat multidirectionnel soit la moins coûteuse possible.

Rigide. adj. (ant. flexible*) Se dit d'un terme dont la tête* est essentiellement universelle*. Un terme rigide ne peut pas changer de forme normale de tête*, alors qu'un terme flexible le peut par l'effet d'une substitution*.

On appelle rigide-rigide une paire de termes tous deux rigides, et rigide-flexible une paire formée d'un premier terme rigide et d'un second terme flexible. On appelle flexible-flexible une paire de termes tous deux flexibles, et flexible-rigide une paire formée d'un premier terme flexible et d'un second terme rigide. On appelle flexible une paire de termes dont un des membres est flexible, et rigide une paire de termes dont les deux membres sont rigides. On appelle rigide un chemin dans un terme qui ne passe par aucun sous-terme flexible, et flexible tout autre chemin.

Par exemple, et en supposant que t est une constante et U est une variable logique, (U t) est un terme flexible et (t (U t)) est un terme rigide. Dans le terme (t U (t (U t))), le chemin de la racine vers le second t est rigide, alors que celui qui va de la racine vers le t le plus à droite est flexible car il traverse le terme flexible (U t).

On appelle rigide une occurrence qui se trouve à l'extrémité d'un chemin rigide, et flexible toute autre occurrence.

Rosser, John Barkley (États-Unis, 1907 -) [Rosser 84]. Rosser étudia les liens entre -calcul* et logique combinatoire*, et la consistance de systèmes logiques fondés sur eux. Il aboutit à la preuve de leur inconsistance en reconstruisant dans le -calcul un paradoxe logique. Il prouva une forme de consistance du -calcul sous la forme du théorème de Church-Rosser* et fut parmi ceux (avec Church*, Curry* et Kleene) qui entrevirent et établirent la complétude calculatoire du -calcul.