Best viewed in 24pt and full-screen

C

type conc (list A) -> (list A) -> (list A) -> o .
conc [] X X .
conc [A|X] Y [A|Z] :- conc X Y Z .
ou
conc L1 L2 L3 :- iter_list L2 er[e|r] L1 L3 .
ou
conc X Y Z :- pi c( pi A(pi X(pi Z(c [A|X] [A|Z] :- c X Z))) => c [] Y => c X Z ) .
ou
type conc_f ((list A)->(list A))->((list A)->(list A))->((list A)->(list A))->o .
conc_f G D z( G (D z) ) .
ou
type conc_d (dlist A) -> (dlist A) -> (dlist A) -> o .
conc_d A-B B-ZB A-ZB .

Plusieurs versions du prédicat de concaténation : classique, avec itérateur*, avec implication, pour listes fonctionnelles*, et pour listes en différence*.

-Calcul. n.m. Calcul dont les termes sont les -termes* et les lois sont celles de la -équivalence*. Le -calcul a été conçu par Church pour remplacer la théorie des ensembles dans son rôle de théorie fondamentale des mathématiques pour éviter les paradoxes d'auto-appartenance. Malheureusement, les mêmes paradoxes peuvent être construits dans le -calcul.

Peu après sa conception, le -calcul se révélera avoir la même puissance de calcul que d'autres formalismes candidats à représenter les fonctions calculables (machine de Turing, etc.) [Rosser 84]. Pour cette raison, et parce que ses termes peuvent être interprétés comme des fonctions, il est le formalisme naturel pour modéliser les langages de programmation fonctionnelle.

Le -calcul a la propriété de Church-Rosser*, mais pas celle de la normalisation forte*.

Church a proposé une variante typée du -calcul [Church 40] pour éviter les paradoxes. À nouveau, ce formalisme n'a pu servir de théorie fondamentale des mathématiques, mais cette fois-ci parce que trop faible. En revanche, il est le plus simple d'une longue liste de formalismes qui peuvent modéliser les types en programmation ( cube de Barendregt*).

-Calcul simplement typé. n.m. Calcul dont les termes sont les -termes simplement typés* et les lois sont celles de la -équivalence*. Le -calcul est le plus simple des calculs du cube de Barendregt*. Il a la propriété de Church-Rosser* et celle de la normalisation forte*.

Calcul des séquents. n.m. (rel. Gentzen*) [Gallier 86, Gallier 91, Lalement 90] Présentation symétrique de règles de déduction* qui permet de raisonner sur les preuves. Le calcul des séquents est défini par un ensemble de règles de déduction qu'il faut juxtaposer pour construire des preuves. Les séquents qu'on peut trouver à la racine d'une preuve sont des théorèmes. Les règles de déduction pour le calcul des prédicats de premier ordre (souvent appelé LK) sont présentées dans la figure 4.

Figure 4: Règles du calcul des séquents LK.

Ici, la virgule qui figure dans les antécédents* et les conséquents* est interprétée comme un constructeur de séquence. Si on l'interprète comme un constructeur de multi-ensembles, on peut oublier les règles d'échange. Si on l'interprète comme un constructeur d'ensembles, on peut aussi oublier les règles de contraction. On peut enfin oublier les règles d'affaiblissement en remplaçant la règle axiome par la suivante.

Dans la suite, et dans les autres articles, on interprète la virgule de façon ensembliste.

Le calcul des séquents est qualifié de symétrique car il traite de la même façon les connecteurs qui apparaissent à gauche et ceux qui apparaissent à droite.

Le principal résultat du calcul des séquents est le Hauptsatz* : la règle de coupure est redondante et peut être éliminée (avec des précautions si des axiomes sont rajoutés au calcul des séquents).

On peut restreindre syntaxiquement les règles du calcul des prédicats de façon à modéliser exactement le calcul des prédicats intuitionniste. Pour cela, il suffit de restreindre les règles d'affaiblissement et de la négation () à droite en exigeant que  soit vide [Kleene 71]. Une autre restriction, plus simple et plus radicale, exige que tous les conséquents soient au plus des singletons. C'est le système qui est souvent appelé LJ. Cette dernière restriction n'est pas nécessaire logiquement, malgré ce qui est souvent laissé entendre. En revanche, elle est commode pour définir des fragments du calcul des séquents interprétables en programmation logique (voir figure 5). Ces restrictions sont équivalentes et il suffirait d'admettre un non-vide dans l'une des deux règles pour retrouver le calcul des prédicats classique.

Figure 5: Règles du calcul des séquents intuitionnistes.

C'est ce calcul qui sert de base logique à Prolog. Il pourrait aussi servir pour Prolog, mais ce n'est pas l'habitude. Dans ce cadre, l'antécédent des séquents modélise le programme et le conséquent modélise le but*. La notion de preuve uniforme* fournit une sémantique opérationnelle pour ces langages. On peut définir d'autres calculs des séquents pour d'autres logiques (par exemple, la logique linéaire [Girard et al. 89]), et pour ces calculs définir une notion de preuve uniforme et rechercher les fragments de ces calculs pour lesquels la prouvabilité uniforme est complète. Miller considère que ces fragments sont tous des langages de programmation logique [Miller 91c, Miller et al. 91].

Church, Alonzo (États-Unis, 1903-1995). Church introduit le -calcul dans les années 1930 comme une notation pour la logique combinatoire ( Curry*) et le développe avec Rosser* et Kleene. Il démontre en 1936 l'indécidabilité du calcul des prédicats [Church 36]. Au passage, il énonce ce qui sera connu comme la «thèse de Church», selon laquelle la théorie des fonctions récursives générales modélise adéquatement la notion de fonction calculable.

Il présente en 1940 une logique d'ordre supérieur [Church 40] dont beaucoup de traits sont représentés en Prolog.

Church (entier de). n.m. Représentation des entiers naturels par des -termes* :

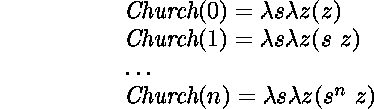
Des représentations similaires peuvent être produites automatiquement pour tous les types inductifs* [Böhm et Berarducci 85, Pierce et al. 89].

On peut spécifier en Prolog la représentation de Church des entiers naturels.

type entier_church ((A->A)->A->A) -> o .

entier_church szz .

entier_church sz( N s (s z) ) :- entier_church N .

On peut remplacer la dernière clause par la suivante,

entier_church sz( s (N s z) ) :- entier_church N .

qui a l'avantage d'appartenir au fragment * de Prolog.

On peut aussi axiomatiser cette représentation à l'aide la quantification universelle :

entier_church N :- pi z( (N xx z) = z ).

On peut remplacer cette clause par la suivante,

entier_church N :- z(N xx z) = zz .

grâce à la correspondance entre quantifications essentiellement universelles*, et plus précisément, grâce à l'axiome de -équivalence*.

Church (Type à la). n.m. Point de vue sur le typage où la vérification du bon typage d'une construction est un préalable à l'énonciation de sa sémantique. Ce point de vue s'oppose à celui dit de Curry*. Il correspond au typage prescriptif* des programmes Prolog.

Church-Rosser. Propriété d'un système de réécriture selon laquelle quand un terme est le point de départ de plusieurs dérivations, elles convergent : ABC[   (A B A C)     D[B D C D]   ].

Le -calcul* a cette propriété, ainsi que tous les calculs du cube de Barendregt*.

Clause. n.f.

1) Dans la forme normale conjonctive* (), une clause est une disjonction de littéraux*. Une formule est une conjonction de clauses.

2) Unité de sens d'un programme Prolog ou Prolog. ( clause définie*)

Clause définie. n.f. (en anglais, definite clause)

1) ( clause de Horn*)

2) Une formule qui a la forme d'une implication dont la tête est atomique et la prémisse quelconque. En ce sens les formules héréditaires de Harrop* sont des clauses définies.

Clause dynamique. n.f. (rel. clause*) Clause ajoutée à un programme par l'effet de l'implication dans les buts de Prolog.

Colmerauer, Alain (France). À la suite de travaux sur le traitement automatique de la langue naturelle, Alain Colmerauer propose d'utiliser comme un langage de programmation le formalisme développé à cette occasion [Colmerauer 70]. Ce formalisme deviendra Prolog* [Battani et Meloni 73, Roussel 75, Colmerauer et al. 79].

Alors que le domaine de calcul de Prolog est celui des termes de premier ordre munis d'une égalité syntaxique, Colmerauer propose d'étendre ce domaine à plus de termes munis de plus de relations. Le système Prolog  étend le domaine aux termes rationnels* munis de l'égalité appropriée et d'une relation de diségalité (dif) [Colmerauer 82, Colmerauer et al. 82, Giannesini et Cohen 84, Van Caneghem 86, Coupet-Grimal 88, Coupet-Grimal 91]. De plus, Prolog  assouplit la stratégie de calcul en donnant le moyen de la faire dépendre du flot de donnée (freeze). Ce système est un premier pas vers la programmation logique avec contraintes. Celle-ci sera réalisée, à Marseille, par les systèmes Prolog  [Colmerauer 90] (contraintes sur les rationnels, les booléens et les chaînes) et Prolog  [Benhamou et Touraïvane 95] (mêmes domaines de contraintes plus intervalles et de nouveaux algorithmes), et par de nombreux autres systèmes dans le monde [Jaffar et Lassez 86, Van Hentenryck 89, Cohen 90].

Alain Colmerauer est actuellement (1998) professeur à l'université d'Aix-Marseille.

Combinateur. n.m.

1) Désigne un -terme qui n'a pas de variables libres*. La situation se complique en Prolog car il y deux sortes de variables : les variables logiques* et les -variables*. En Prolog, on appelle combinateur un -terme qui n'a pas de -variables libres même s'il contient des variables logiques libres. Cette notion a un rôle important dans la pragmatique de Prolog [Belleannée et al. 95] et dans son implémentation [Brisset et Ridoux 91].

D'un point de vue pragmatique, il est important de voir que le domaine de calcul de Prolog est uniquement composé de combinateurs ; tous les paramètres de prédicat, et toutes les variables logiques désignent des combinateurs. En particulier, il n'y a aucun moyen direct de manipuler le corps d'une abstraction si celui-ci n'est pas dégénéré et comporte bien des occurrences libres de la variable abstraite. De plus, la propriété d'être un combinateur est conservée par les substitutions solutions du problème d'unification des -termes simplement typés. Les combinateurs détectés à la compilation seront donc toujours des combinateurs lors de l'exécution. Noter que les sous-termes d'un combinateur peuvent ne pas être des combinateurs s'ils ne sont pas passés en paramètre d'un prédicat, et s'ils ne sont pas substitués à une variable logique.

La détection des combinateurs est importante car elle donne un critère pour améliorer la procédure de -réduction*. En effet, alors que la réduction de graphes* naïve duplique le terme de gauche d'un -rédex*, ses sous-termes qui sont des combinateurs peuvent être partagés sans autre précaution. Nos expériences ont montré que cette heuristique apporte un gain de complexité et augmente la réutilisation des structures de données, et donc le partage de représentation* (voir la section «Le rôle des combinateurs»*).

2) Désigne un terme de la logique combinatoire*. Les deux acceptions sont cependant très proches.

Compilation de l´implication. n.f. ( implication*) La lecture opérationnelle de la règle de déduction de l'implication à droite ( calcul des séquents*) est que prouver un but dans un programme  nécessite de prouver le but  dans le programme  augmenté de la clause . Cette lecture laisse penser que le programme est une entité dynamique qui peut difficilement être compilée.

En fait, on peut compiler séparément les clauses dynamiques* et les ajouter à la demande au programme par une sorte d'édition de lien dynamique. Comme les clauses dynamiques peuvent contenir des variables libres, ce qui est réellement compilé est une clôture des clauses. Cela peut être formalisé de la manière suivante.

Une clause dynamique d'un prédicat avec les variables libres est compilée en , où est une constante nouvelle. L'ajout de la clause dynamique dans un contexte où les variables libres valent introduit la paire dans la continuation de programme*. L'exécution d'un but recherche les paires <p,c> et appelle , soit qui fait le lien à la fois avec les paramètre effectifs () et avec le contexte où sont définies les variables libres de la clause ().

Conclusion. n.f. ( règle de déduction*)

Condition de tête. n.f. (parfois appelée «généricité définitionnelle» pour definitional genericity) La condition de tête prescrit que toutes les occurrences d'un même symbole prédicatif en tête de clause ont des types qui sont des renommages du schéma de type du symbole prédicatif. Cette condition s'ajoute donc à la condition de typage «à la » qui prescrit que les occurrences d'un symbole ont des types qui sont des instances indépendantes du schéma de type du symbole. Cette condition élimine un style de programmation courant en Prolog non typé dans lequel contenant et contenu (par exemple, listes et éléments) sont traités par le même prédicat, et elle rend l´inférence de type* équivalente au problème de semi-unification non-uniforme et donc indécidable [Kfoury et al. 93]. Néanmoins, cette condition est nécessaire pour que le typage cohabite harmonieusement avec des manipulations de programmes importantes et avec la modularité des programmes ( typage paramétrique*).

La condition de tête est admise implicitement dans le système de types pour Prolog de Mycroft et O'Keefe [Mycroft et O'Keefe 84]. Elle figure sous le nom de «condition de tête» (head condition) dans les propositions de Hanus, et de Hill et Lloyd [Hanus 91, Hill et Lloyd 94], et sous le nom de «généricité définitionnelle» (definitional genericity) dans la proposition de Lakshman et Reddy [Lakshman et Reddy 91]. Cette condition n'est pas décrite dans la définition de Prolog et elle est écartée dans la proposition de Nadathur et Pfenning [Nadathur et Pfenning 92]. Elle est adopté dans l'implémentation * de Prolog.

Beaucoup de programmes classiques en Prolog non-typé violeraient la condition de tête si on les typait. Ces programmes correspondent souvent à des pratiques qui ne sont pas déclaratives et qui sont condamnables même dans le cas non-typé [O'Keefe 90]. Il subsiste des cas où les programmes interdits sont légitimes, mais une discipline de typage paramétrique* accepte ces programmes.

Condition de transparence. n.f. Condition selon laquelle les variables de type* qui apparaissent dans une déclaration de type doivent apparaître dans le type résultat. Conjointement avec la condition de tête* cette condition permet de démontrer un théorème de correction sémantique* pour Prolog.

On dit d'un type déclaré qui ne vérifie pas la condition de transparence qu'il oublie les variables de type qui n'apparaissent pas dans le type résultat. On dit des instances de ces variables que ce sont des types oubliés*.

Par exemple, les types de nil ((list A)) et cons (A->(list A)->(list A)) vérifient la condition de transparence : la seule variable, A, apparaît dans le type résultat. Le type de conc ((list A)->(list A)->(list A)->o) ne la vérifie pas, et plus généralement aucun type de prédicat polymorphe ne la vérifie. En effet, la variable A n'apparaît pas dans le type résultat, o.

Conséquent. n.m. ( séquent*)

Constante universelle. n.f. (rel. élimination des quantificateur*) (en anglais, eigen-value) Constante utilisée pour éliminer une quantification essentiellement universelle*. Elle doit être nouvelle, c'est-à-dire ne pas avoir d'occurrence libre* dans la formule quantifiée ou dans son contexte (voir aussi les règles du calcul des séquents* : introduction à droite de la quantification universelle et à gauche de la quantification existentielle).

Constructeur de termes. n.m. (rel. type simple*) Symbole fonctionnel qui peut être appliqué à des arguments dont la nature dépend du domaine de termes en vigueur pour former un terme. Par exemple, dans un domaine de premier ordre*, les arguments doivent être des termes en même nombre que l´arité* du constructeur. Dans un domaine de termes typés, les arguments doivent en plus avoir des types compatibles avec le type du constructeur de terme.

En Prolog*, les constructeurs de termes sont introduits par la déclaration type. Par exemple la déclaration suivante

type abs (l_terme->l_terme) -> l_terme .

introduit le constructeur de terme abs et spécifie qu'il peut être appliqué à un terme de type l_terme->l_terme pour former un terme de type l_terme.

Constructeur de types. n.m. (rel. type simple*) Dans un langage typé, symbole fonctionnel qui peut être appliqué à des arguments dont la nature dépend du langage pour former un type.

En Prolog*, les constructeurs de types sont introduits par la déclaration kind. Par exemple, la déclaration suivante

kind list type -> type .

introduit le constructeur de type list et spécifie qu'il doit être appliqué à un type pour former un type.

Continuation. n.f. Structure de données abstraite qui permet de formaliser le contrôle des langages de programmation en notant les calculs qu'il reste à faire. Les continuations ont été introduites pour décrire le contrôle des langages de programmation impératifs, puis fonctionnels, puis logiques.

Dans les deux premiers cas, une continuation suffit, mais dans le cas de la programmation logique, deux sont nécessaires [Nicholson et Foo 89, Consel et Khoo 91]. L'une correspond à la résolvante* et est appelée la continuation de succès (que faire en cas de succès ?), l'autre correspond à la pile de recherche* et est appelée la continuation d'échec (que faire en cas d'échec ?).

Les équations suivantes présentent un système d'équations qui définit la sémantique de Prolog en termes de continuations. La continuation de succès (notée ) détermine le calcul à faire à la suite du succès d'un but. On la voit passée en paramètre dans la traduction d'un but élémentaire, , et on voit sa construction dans la traduction d'un but complexe, . La condition d'échec (notée ) détermine le calcul à faire à la suite de l'échec d'un but. On la voit passée en paramètre dans la traduction d'un but élémentaire, et on voit sa construction dans la traduction d'une conjonction de clauses d'un même prédicat, . L'unification est représentée par la constante , et on peut voir dans sa spécification comment les deux continuations sont exploitées lors du succès ou de l'échec de l'unification. Partout, la variable  représente les paramètres effectifs d'un appel à un prédicat.

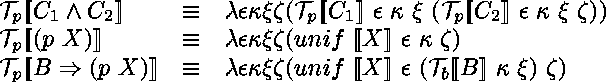
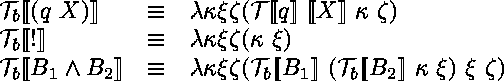
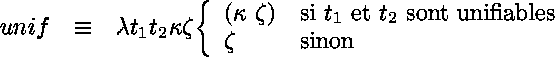
Comme cela a été fait pour les langages de programmation fonctionnels, on peut capturer (réifier*) les continuations de la programmation logique afin de modéliser la coupure* et la gestion d'exceptions [Brisset 92, Brisset et Ridoux 93]. Tous les systèmes Prolog proposent la coupure, et beaucoup la gestion d'exceptions, mais il est difficile de modéliser ces deux mécanismes dans le cadre de la sémantique opérationnelle basée sur la résolution*. Cela devient assez simple dans le modèle des continuations. La continuation d'échec à l'entrée dans un prédicat est capturée dans une variable  dans la traduction d'une clause, , et elle est réfléchie* dans la continuation d'échec dans la traduction de la coupure, . Dans celle-ci, la continuation d'échec en entrée, , est ignorée et remplacée par la continuation d'échec capturée, .

Il faut noter que cette sémantique spécifie l'ordre de sélection des clauses et des buts, ce que la sémantique de Prolog basée sur la résolution ne fait pas. La sémantique basée sur les continuations est donc plus fidèle à la majorité des systèmes Prolog, mais elle permet difficilement de rendre compte de stratégies plus dynamiques sauf à écrire l'équivalent d'un ordonnenceur de buts et de clauses en -calcul. Ce surcroît de précision est toutefois nécessaire pour donner la sémantique de la coupure.

On peut imaginer une variante de la coupure inspirée de la capture de continuation en Scheme. Un prédicat call_fc permet d'appeler un but en lui passant la continuation d'échec en paramètre (réification), et un prédicat cut prend en paramètre une continuation d'échec capturée et l'installe comme continuation d'échec courante (réflexion).

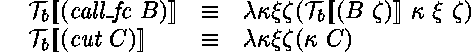
Quand on passe à Prolog, la situation se complique car il faut tenir compte de la sémantique des clauses ajoutées par implication, et des quantifications universelles. Pour cela on ajoute deux nouvelles continuations. L'une, , est destinée à gérer l'évolution du programme, l'autre, , celle de la signature. Les équations suivantes donnent la sémantique de Prolog en termes de continuations. La continuation de signature est essentiellement un entier qui permet de produire des toujours nouveaux dans une même branche de preuve (voir l'équation pour ). La continuation de programme est un tableau de dénotations de paquets de clauses dynamiques* indexé par les prédicats. On écrira donc pour désigner les clauses dynamiques du prédicat . À chaque fois qu'une clause est ajouté à un prédicat, sa dénotation est composée avec celle du paquet de clauses dynamiques de ce prédicat (voir l'équation pour ).

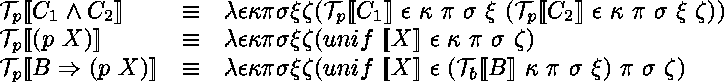
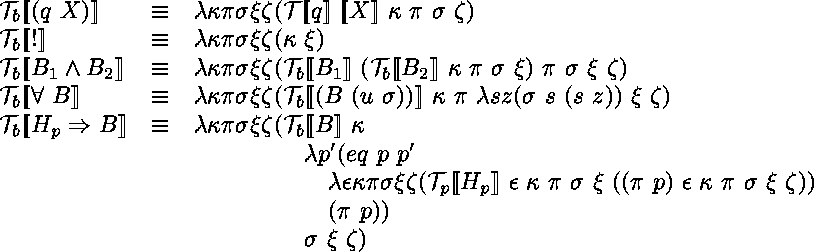
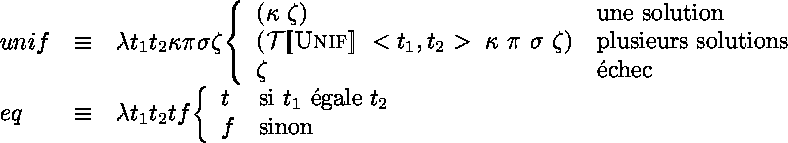
La définition de fait référence à un prédicat qui est sensé implémenter l´unification d´ordre supérieur*. Cela permet de sous-traiter à la sémantique des prédicats la gestion de l'indéterminisme du problème d'unification. C'est ce qui est fait dans le système *.

Ici encore, la sémantique basée sur les continuations fixe un ordre de sélection des clauses dynamiques, alors que celle qui est basée sur le calcul des séquents n'en fixe aucun. Cependant, la sémantique basée sur les continuations précise un comportement possible de la coupure vis-à-vis des clauses dynamiques (le comportement effectif du système ).

Correction sémantique. n.f. Propriété d'une classe de programmes typés dont l'exécution ne peut pas causer d'erreurs de type s'ils sont bien typés, «Well-typed programs cannot go wrong» [Milner 78].

Les programmes de cette classe n'ont pas besoin que les types soient représentés à l'exécution. Inversement, les autres programmes ont besoin que des types soient représentés à l'exécution, mais pas forcément tous.

Dans le cas de Prolog*, le résultat est le suivant : un programme qui vérifie la condition de transparence*, est constitué de clauses bien typées et dont les prédicats vérifient la condition de tête*, ne peut pas causer d'erreur de type à l'exécution [Hanus 91].

Coupure. n.f.

1) Règle du calcul des séquents* qui modélise l'utilisation d'un lemme dans une démonstration ( Hauptsatz*).

2) Opérateur de contrôle de la stratégie de recherche de Prolog noté «!» dans la syntaxe standard*. Il permet d'élaguer l'arbre de recherche.

Currifier. v. tr. Représenter une fonction à  paramètres, , par une fonction qui prend le premier paramètre et qui rend une fonction qui prend le deuxième paramètre, etc., (ou plus simplement ). Cette possibilité observée d'abord par Frege, puis Shönfinkel, est couramment attribuée à Curry*. Elle trouve une généralisation dans la notion d'isomorphisme de type [Di Cosmo 95].

Curry, Haskell Brooks (États-Unis, 1900-1982). Haskell Curry est le principal contributeur de la logique combinatoire [Curry et al. 68]. Cette logique est intimement reliée au -calcul* [Hindley et Seldin 86], et son influence va jusqu'à la programmation fonctionnelle [Revesz 88].

Curry (type à la). n.m. Point de vue sur le typage où le bon typage est une propriété complètement indépendante de la sémantique. Il n'est pas nécessaire qu'un programme soit bien typé pour lui donner une sémantique. Ce point de vue s'oppose à celui dit de Church*. Il correspond au typage descriptif* des programmes Prolog.

Curry-Howard (correspondance/isomorphisme de). La correspondance de Curry-Howard formalise le parallèle entre types et termes d'une part, et formules et preuves d'autre part [Curry et al. 68, Howard 80]. Cette correspondance est plus ou moins étroite selon les systèmes logiques, et elle constitue même parfois un isomorphisme [Barendregt et Hemerik 90, Barendregt 91]. Par exemple, le -calcul simplement typé* est en correspondance de Curry-Howard avec le fragment du calcul propositionnel intuitionniste muni de la seule implication : la flèche de type correspond à l'implication, les -termes simplement typés* correspondent aux preuves en déduction naturelle. Des systèmes de type plus riches (par exemple, ceux du cube de Barendregt*) correspondent à des logiques munies de plus de connecteurs. Avec des systèmes de types trop riches, la correspondance ne peut être utilisée que comme une métaphore.

Dans le cadre de la programmation, la correspondance de Curry-Howard s'étend aux spécifications et aux programmes : un programme (correct) est la preuve qu'une spécification est réalisable (dans le langage de programmation correspondant au langage des preuves), de la même façon qu'un terme (bien typé) est la preuve qu'un type est habité. Dans ce cadre [Huet et al. 97], on fait jouer aux types le rôle de spécifications et un démonstrateur automatique en extrait un programme. Deux problèmes se font jour : la spécification peut ne pas être réalisable dans le langage des preuves du système logique, ou bien la spécification est réalisable, mais pas par un algorithme raisonnable.