Best viewed in 24pt and full-screen




Next: V-W
Up: A-Z
Previous: T
kind ulist type -> type -> type .
type ucons A -> (ulist B R) -> (ulist A->B R) .
type unil (ulist R R) .
type univ A -> (ulist B->B A) -> o .
Par exemple : univ (1 + 2) (ucons (+) (ucons 1 (ucons 2 unil)))
Typage du prédicat prédéfini univ (aussi noté =..). L´homogénéité du type des constructeurs de liste habituels ( déclaration list*) ne permet pas de construire une liste d´une fonction et de ses arguments. Le premier type passé en paramètre de ulist est celui d´une fonction qui peut prendre en paramètre les termes rangés dans la liste. Le deuxième type est celui du résultat, en fait le type du terme passé en premier paramètre de univ. Ce typage ne convient que pour une réalisation intentionnelle (par le système) de univ. Une réalisation extensionnelle (par une relation explicite) violerait la condition de tête.
déclaration list*) ne permet pas de construire une liste d´une fonction et de ses arguments. Le premier type passé en paramètre de ulist est celui d´une fonction qui peut prendre en paramètre les termes rangés dans la liste. Le deuxième type est celui du résultat, en fait le type du terme passé en premier paramètre de univ. Ce typage ne convient que pour une réalisation intentionnelle (par le système) de univ. Une réalisation extensionnelle (par une relation explicite) violerait la condition de tête.
 Unification.
n.f.
(rel. Herbrand* et substitution*)
Problème de vérifier si il existe une substitution de leurs variables
qui peut rendre deux termes égaux,
ou équivalents modulo une relation donnée
(par exemple, par une théorie équationnelle),
et de produire une telle substitution quand elle existe (un unificateur).
Par exemple,
le résultat de l'unification de
Unification.
n.f.
(rel. Herbrand* et substitution*)
Problème de vérifier si il existe une substitution de leurs variables
qui peut rendre deux termes égaux,
ou équivalents modulo une relation donnée
(par exemple, par une théorie équationnelle),
et de produire une telle substitution quand elle existe (un unificateur).
Par exemple,
le résultat de l'unification de
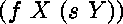 et de
et de
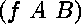 est qu'il existe une substitution qui les rend égaux
et qu'elle peut être
est qu'il existe une substitution qui les rend égaux
et qu'elle peut être 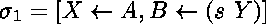 ,
ou
,
ou
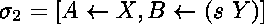 ,
ou bien
,
ou bien
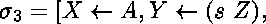
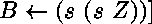 ,
ou encore
,
ou encore
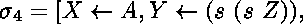
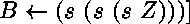 , etc.
Inversement,
le résultat de l'unification de
, etc.
Inversement,
le résultat de l'unification de 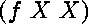 et de
et de
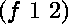 est qu'il n'existe pas de substitution qui les rend égaux.
est qu'il n'existe pas de substitution qui les rend égaux.
Quand une telle substitution existe,
il peut en exister plusieurs et même une infinité.
On ignore donc les variantes dues aux noms des variables,
comme 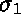 et
et 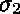 ,
et on se restreint aux unificateurs les plus généraux
(
,
et on se restreint aux unificateurs les plus généraux
(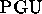 ).
Ce sont des unificateurs tels
que tout autre unificateur résulte de la composition d'un unificateur
plus général et d'une substitution.
Les substitutions
).
Ce sont des unificateurs tels
que tout autre unificateur résulte de la composition d'un unificateur
plus général et d'une substitution.
Les substitutions 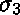 et
et 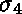 ne sont pas plus générales :
elles résultent de la composition de
ne sont pas plus générales :
elles résultent de la composition de 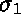 et de
et de
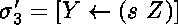 ou
ou
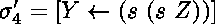 .
En définitive,
.
En définitive,
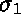 et
et 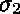 sont plus générales,
mais équivalentes aux noms des variables près.
sont plus générales,
mais équivalentes aux noms des variables près.
Selon le domaine de terme et sa théorie de l'égalité,
le nombre d'unificateurs plus généraux varie ;
il peut y en avoir au maximum un,
le problème est alors qualifié d'unitaire,
plusieurs mais en nombre fini,
le problème est alors qualifié de finitaire,
ou même une infinité,
le problème est alors qualifié d'infinitaire.
Par exemple,
le problème d'unification des termes de premier ordre est unitaire,
alors que le problème
d´unification des termes d´ordre supérieur*
est infinitaire.
On peut s'en convaincre en résolvant l'équation suivante en
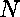 :
:
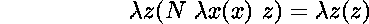
Les solutions sont  ,
, 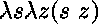 ,
,
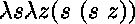 , ...,
, ..., 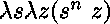 .
Ces termes sont les entiers de Church*.
Il y en a naturellement une infinité,
et aucun n'est une instance d'un autre.
.
Ces termes sont les entiers de Church*.
Il y en a naturellement une infinité,
et aucun n'est une instance d'un autre.
La résolution effective de ces problèmes n'est pas toujours possible.
Les problèmes qui nous intéressent sont soit décidables*
comme le problème d'unification des termes du premier ordre
avec égalité syntaxique,
soit semi-décidables*
comme le problème d'unification des termes d'ordre supérieur.
 Unification d´ordre supérieur.
n.f.
Problème de vérifier si il existe une substitution
qui peut rendre deux
Unification d´ordre supérieur.
n.f.
Problème de vérifier si il existe une substitution
qui peut rendre deux  -termes*
égaux modulo la
-termes*
égaux modulo la  -équivalence*,
et de produire une telle substitution quand elle existe (un unificateur).
Pour le
-équivalence*,
et de produire une telle substitution quand elle existe (un unificateur).
Pour le  -calcul simplement typé*,
le problème est infinitaire*
et semi-décidable*.
La première procédure a été proposée par
Huet [Huet 75] :
semi-algorithme de Huet*.
D'autres présentations en ont été faites par
Snyder et Gallier [Snyder et Gallier 89] et par
Paulson et Nipkow [Paulson 86, Nipkow 90].
Miller a étudié la correspondance entre quantifications logiques
(
-calcul simplement typé*,
le problème est infinitaire*
et semi-décidable*.
La première procédure a été proposée par
Huet [Huet 75] :
semi-algorithme de Huet*.
D'autres présentations en ont été faites par
Snyder et Gallier [Snyder et Gallier 89] et par
Paulson et Nipkow [Paulson 86, Nipkow 90].
Miller a étudié la correspondance entre quantifications logiques
( and
and  ) et la quantification du
) et la quantification du
 -calcul*
(
-calcul*
( -abstraction*) [Miller 92].
Elliot, Pym et Pfenning ont exploré l'unification d'ordre supérieur dans le
cube de Barendregt* [Elliott 89, Pfenning 91, Pym 92].
-abstraction*) [Miller 92].
Elliot, Pym et Pfenning ont exploré l'unification d'ordre supérieur dans le
cube de Barendregt* [Elliott 89, Pfenning 91, Pym 92].
 Unificateur.
n.m.
Solution d'un problème
d´unification*.
C'est une
substitution*.
Unificateur.
n.m.
Solution d'un problème
d´unification*.
C'est une
substitution*.
 Unitaire.
adj.
Unitaire.
adj.
1)
( unification*)
unification*)
2)
( clause unitaire*).
clause unitaire*).




Next: V-W
Up: A-Z
Previous: T
Olivier Ridoux
Mon Apr 27 11:10:23 MET DST 1998
 Unification.
n.f.
(rel. Herbrand* et substitution*)
Problème de vérifier si il existe une substitution de leurs variables
qui peut rendre deux termes égaux,
ou équivalents modulo une relation donnée
(par exemple, par une théorie équationnelle),
et de produire une telle substitution quand elle existe (un unificateur).
Par exemple,
le résultat de l'unification de
Unification.
n.f.
(rel. Herbrand* et substitution*)
Problème de vérifier si il existe une substitution de leurs variables
qui peut rendre deux termes égaux,
ou équivalents modulo une relation donnée
(par exemple, par une théorie équationnelle),
et de produire une telle substitution quand elle existe (un unificateur).
Par exemple,
le résultat de l'unification de