Best viewed in 24pt and full-screen

Le rôle des combinateurs

La -réduction* est une opération fondamentale de Prolog, et elle se fait principalement à la demande de l'unification pour normaliser les termes à comparer et accessoirement à la demande du programmeur pour rendre les termes plus lisibles ou plus compacts.

Le problème posé en Prolog diffère beaucoup de celui posé pour les langages de programmation fonctionnelle. En général, ces derniers «ne réduisent pas sous les lambdas», alors qu'en Prolog il faut presque toujours le faire. Cela vient de ce que les langages de programmation fonctionnelle ne permettent pas de comparer des fonctions, alors que cette opération est au cur de Prolog. En Prolog, la -réduction doit être combinée avec la substitution de variable logique* et le retour-arrière. Dans cette combinaison, la -réduction peut produire des formes normales dites flexibles* que la substitution de variable logique peut rendre non-normales. De plus, le retour-arrière peut inverser toutes les transitions de normale à non-normale et vice-versa. Enfin, en Prolog, aucune opération à effet de bord n'est attachée à la -réduction et le -calcul utilisé, le -calcul simplement typés*, est fortement normalisable* ; l'ordre de -réduction est donc absolument quelconque, y compris d'une fois sur l'autre.

Nous avons choisi de représenter les -termes par des graphes, et d'implémenter la -réduction par réduction de graphe*. C'est une autre différence avec le projet de Gopalan Nadathur [Nadathur et Wilson 90] où il est prévu d'employer la représentation de de Bruijn* et des environnements représentant les substitutions de -variable. En fait, il ne faut pas trop insister sur ces différences, car pas plus Gopalan Nadathur et ses collègues que nous, n'avons pensé utiliser un schéma pur. Par exemple, nous combinons la réduction de graphe avec des notations de substitution explicite* et Nadathur envisage la substitution in-situ de -rédex*.

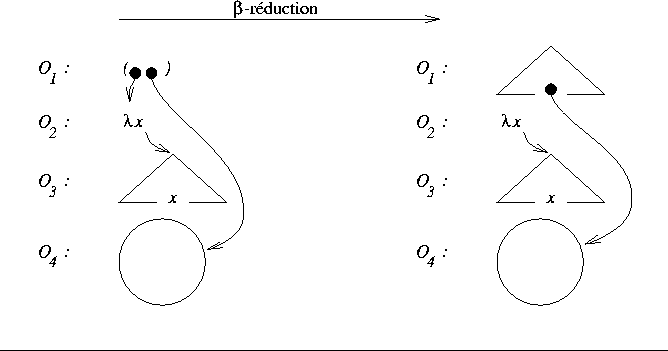
Figure 2: Réduction de graphe naïve

Implémenter la réduction de graphe est assez simple, mais ne doit pas être fait trop naïvement. En effet, la -réduction duplique la représentation du membre gauche du -rédex*, car celui-ci peut être utilisé dans d'autres termes. C'est par exemple le cas lorsqu'une fonction est appliquée à plusieurs jeux d'arguments : il ne faut pas que l'évaluation de la première application change la valeur de la fonction. La figure 2 illustre la réduction de graphe et la duplication du membre gauche du -rédex. Dans cette figure et dans les suivantes, les sont des objets de la représentation. Les parties gauche et droite de la figure schématisent respectivement l'état de la représentation avant et après la -réduction. Les objets , et restent inchangés, et c'est nécessaire car ils peuvent être utilisés dans d'autres contextes. L'objet est transformé. Il contient initialement une notation d'application, et donc de -rédex puisque son membre gauche est une -abstraction. Après la -réduction, il contient une copie de l'objet où les occurrences de la variable x sont remplacées par une référence à l'objet . C'est ce remplacement qu'on ne peut pas effectuer dans l'original car celui-ci doit pouvoir resservir.

On peut observer que si on sait que ne contient pas d'occurrences de la variable x, la procédure de remplacement ne risque pas de modifier  : on peut donc le partager plutôt que le dupliquer. La figure 3 illustre cette possibilité dans le cas dégénéré où la variable x n'a pas d'occurrences dans . La situation générale est celle où contient des occurrences de la variable x et des sous-termes sans occurrences de x (voir la figure 4). On veut alors dupliquer la partie de qui contient les occurrences de x et partager les autres sous-termes. Dans la figure, ces sous-termes sont schématisés par l'objet .

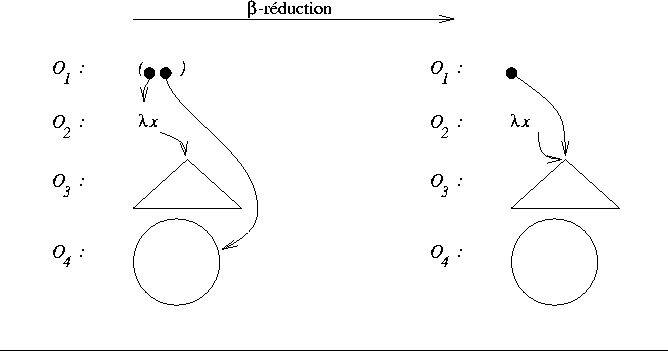
Figure 3: Réduction de graphe avec partage de combinateurs (cas dégénéré)

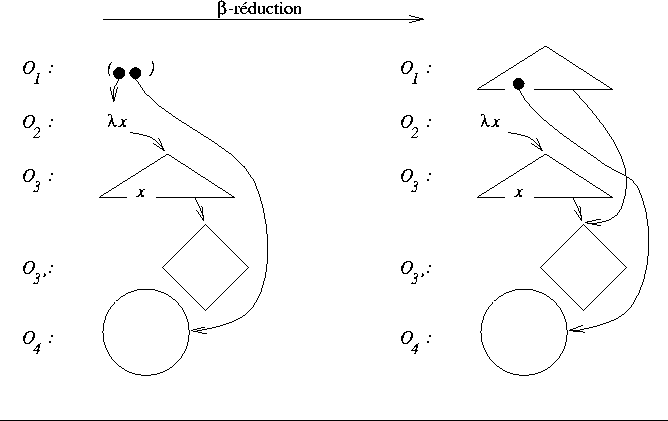
Figure 4: Réduction de graphe avec partage de combinateurs (cas général)

Puisque le coût d'une exploration et le coût d'une duplication sont similaires, on ne gagnerait rien à détecter l'absence d'occurrence de la variable à substituer à chaque -réduction par une exploration. Il faut donc trouver un moyen de connaître les -variables contenues libres dans un terme, sans avoir à l'explorer. Noter exactement et sans explorations répétées cette information dans chaque sous-terme est impossible car ce n'est pas une propriété stable par instanciation et -réduction. Cependant, il existe une approximation de cette propriété qui est stable par instanciation et -réduction : c'est le fait qu'un terme ne contient aucune -variable libre. Un tel terme est un combinateur*, et une marque binaire suffit à le noter. Elle est calculée dès la compilation, et ensuite propagée par des règles simples aux termes qui se construisent à l'exécution. Ce faisant, on renonce à partager tout ce qui peut l'être, et on évite de dupliquer uniquement les termes qui ne contiennent aucune variable libre au lieu de ceux qui ne contiennent aucune occurrence libre de la variable à substituer.

On peut se demander si cette approximation n'est pas trop grossière. En fait, il n'en est rien, et c'est là que la compréhension de l'implémentation et celle du langage s'enrichissent mutuellement. L'idée est qu'il y a énormément de combinateurs lors de l'exécution simplement parce qu'ils constituent le «vrai» domaine de calcul de Prolog. En effet, les variables logiques ne peuvent être instanciées que par des combinateurs, et il n'y a pas de -variables* libres dans une formule logique. Cela a deux conséquences : une pour l'implémenteur et une autre pour le programmeur.

Au niveau du schéma d'exécution, la conséquence est que se limiter à reconnaître les combinateurs plutôt que les occurrences libres de chaque variable dans chaque sous-terme est un bon compromis. Par exemple, dans le cadre d'une représentation fonctionnelle* des listes, le prédicat de renversement de liste a la forme suivante :

type ((list A)->(list A)) -> ((list A)->(list A)) -> o .

renv xx yy .

renv x[A | (L x)] y(R [A | y]) :- renv L R .

Nous avons choisi de donner des noms différents aux différentes -variables liées dans une même clause pour pouvoir les désigner par leur nom dans le commentaire. Cela n'est absolument pas nécessaire en Prolog. Au contraire, nous recommandons de donner systématiquement le même nom aux variables qui jouent le même rôle.

Dans la seconde clause, la variable logique A ne peut désigner qu'un combinateur, et en particulier, elle ne peut contenir d'occurrence libre ni de y ni de x. Cette variable représente un élément d'une liste fonctionnelle, et récursivement toute la liste est constituée d'éléments qui sont des combinateurs. Ainsi, lorsque la liste R est appliquée à [A|y], seul son squelette devra être dupliqué.

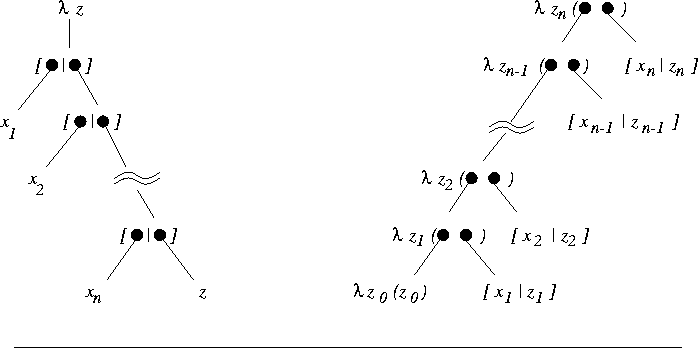
Figure: Listes fonctionnelles peignées : à droite, à gauche

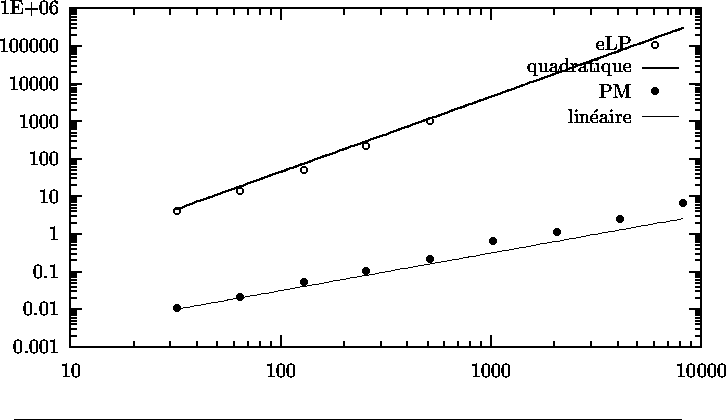
Figure: Comparaison de temps de calcul pour renverser une liste fonctionnelle, sun4, 32 Mo (longueur de la liste  temps de calcul en secondes, échelle log-log)

Mieux, grâce à la paresse du -réducteur, la liste R a la forme de

plutôt que de . En d'autres termes, elle est peignée à gauche par des applications au lieu d'être peignée à droite par des constructeurs (voir la figure 5). Tout ce qui est souligné est un combinateur car c'est une instance de la variable logique R au rang n-1. On voit donc qu'à chaque itération le rédex du second argument de renv ne nécessite de dupliquer qu'une application et un cons. On obtient ainsi des améliorations de complexité, et on atteint même dans cet exemple la complexité linéaire attendue (voir la figure 6 et [Brisset et Ridoux 91, Brisset et Ridoux 94]). Les deux axes de la figure 6 utilisent une échelle logarithmique. Cela permet de représenter des écarts d'amplitude très grands, et de visualiser la complexité effective des calculs de et en comparant simplement les pentes de deux droites (1 pour linéaire, 2 pour quadratique).

Tout ceci résulte d'une analyse purement locale. Une analyse globale permettrait de détecter que tout ou partie du corps d'une -abstraction n'est de toute façon pas utilisé ailleurs que dans ce -rédex et qu'on peut donc le modifier in-situ sans risque. C'est un champ de recherche en cours d'exploration [Malésieux et al. 98].

L'autre conséquence de ce qu'il n'y a pas de -variables* libres dans une formule logique se situe au niveau de la programmation : on ne peut pas «parler» directement de termes qui ne sont pas des combinateurs. Or, on a besoin de «parler» de termes contenant des variables libres, ne serait-ce que pour exprimer une propriété par induction sur la structure des -termes ( induction structurelle*). Un combinateur qui est une abstraction peut avoir des sous-termes qui ne sont pas des combinateurs. C'est même le cas le plus fréquent car autrement ce serait une abstraction triviale qui n'utiliserait pas les variables qu'elle lie. Le moyen de parler de termes avec -variables libres sans jamais en citer explicitement est fourni par une correspondance très importante entre -abstraction et quantification universelle dans les buts : ce sont toutes deux des quantifications essentiellement universelles*. En utilisant cette correspondance, les constantes universelles représentent les -variables libres, mais n'en sont pas. Cela permet de représenter des termes avec -variables libres par des combinateurs.