EP-ATR

Le principe de transformation des programmes Signal permet de décomposer un programme en une partie décrivant le contrôle booléen et une partie contenant les calculs. Le contrôle lui-même définit un système dynamique qui peut être étudié sous plusieurs aspects à des fins de vérification et de synthèse : étude de l'ensemble des états admissibles (partie statique), pour laquelle une forme canonique arborescente utilisant des BDD a été définie; calcul dynamique s'appuyant sur la représentation équationnelle d'un automate.

En appliquant le principe de transformation, on décompose un programme Pen une partie Q(P) contenant le contrôle booléen et une partie C(P)contenant les calculs non booléens, telles que P = Q(P)| C(P).

Toute propriété de sûreté, qui peut s'exprimer sous la forme d'un programme Signal R, satisfaite par Q(P), ce qui s'exprime sous la forme R| Q(P) = Q(P), est également satisfaite par P, puisqu'il résulte de P = Q(P)| C(P)que P = Q(P)| P.

À une équation purement booléenne I correspond Q(I) = I; C(I) est alors l'élément neutre du monoïde.
D'une équation monocadencée, est extraite par Q la partie synchronisation des signaux; on obtient par exemple pour

 
              x := y+z

l'expression :
x ^= y ^= z | x := y+z
(x ^= y ^= z} spécifie l'égalité des horloges de x, y et z).
Une équation de la forme x := y when b, dans laquelle x est non booléen, est décomposée en :

 
              x ^= (y when b) | x := y when b

.
Une équation de la forme x := y default z, dans laquelle x est non booléen, est décomposée en :

 
              x ^= (y default z) | x := y default z

Cette interprétation permet donc d'extraire, de façon automatique, par Q(P), l'aspect système à événements discrets, du système hybride spécifié par le programme. En raison de l'opérateur de retard qui introduit des indices temporels différents, le système est dynamique.

L'étude de ces systèmes dynamiques repose sur l'utilisation de techniques algébriques sur les corps de Galois. Elle vise à exprimer les propriétés des systèmes dynamiques et à donner une solution algorithmique pour leur vérification et pour la synthèse de systèmes satisfaisant certaines spécifications.

Q(P) est défini sur trois valeurs :

{ 
              vrai, faux, absent }

. La sémantique des opérateurs de Signal et l'approche flot de données équationnelle conduisent naturellement à un codage de Q(P) en équations polynomiales sur le corps $\mathbb{Z}$ /3 $\mathbb{Z}$ (ou ${\cal F}_3$ ), vrai, faux, absent étant représentés respectivement par 1, - 1, 0 (+ est l'addition modulo 3, x est la multiplication usuelle).

L'étude de la sémantique abstraite d'un programme Signal se ramène alors à l'étude des systèmes dynamiques polynomiaux de la forme :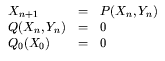

$\displaystyle \left\{\vphantom{ \begin{array}{lcl} X_{n+1}&=&P(X_n,Y_n)\\ Q(X_n,Y_n)&=&0 \\ Q_0(X_0)&=&0 \end{array}}\right.$ $\displaystyle \begin{array}{lcl} X_{n+1}&=&P(X_n,Y_n)\\ Q(X_n,Y_n)&=&0 \\ Q_0(X_0)&=&0 \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{lcl} X_{n+1}&=&P(X_n,Y_n)\\ Q(X_n,Y_n)&=&0 \\ Q_0(X_0)&=&0 \end{array}}\right.$

Un tel système dynamique n'est qu'une forme particulière de système de transitions à espace d'états finis. C'est donc un modèle de système à événements discrets sur lequel il est possible de vérifier des propriétés [MLB96] ou bien de faire du contrôle.

Différentes techniques ont été développées pour ces deux problèmes. Les contraintes statiques sont essentielles pour la compilation des programmes Signal, et des techniques très efficaces ont été développées pour cela. La partie dynamique demande plus de calculs, et est utilisée principalement pour la vérification de propriétés; une technique plus générale -- mais en retour moins efficace -- a été développée pour la prendre en compte.

Le calcul d'horloges statique est au coeur du compilateur Signal; il en détermine largement ses performances. Ce calcul s'appuie sur l'ordre partiel des horloges, qui correspond à l'inclusion des ensembles d'instants (une horloge pouvant être plus fréquente qu'une autre).

La situation suivante doit être considérée : H est l'horloge d'un signal, par exemple un signal à valeurs réelles X, et K est l'ensemble des instants où le signal X dépasse un seuil :

 K := 
              when (X > X_MAX)

. Alors 1/ chaque instant de

est un instant de H , et 2/ pour calculer le statut de K, il faut d'abord connaître le statut de H . Il y a donc à la fois le fait que

est moins fréquent que H et qu'il existe une contrainte de causalité de H vers K . Ceci est dénoté par H $\rightarrow$ K . De tels sous-échantillonnages successifs organisent les horloges en plusieurs arbres, l'ensemble de ces arbres constituent la forêt d'horloges du programme considéré. Si un seul arbre est obtenu, la synchronisation du programme et son exécution s'en déduisent aisément.

La forêt associée à un programme donné n'est pas unique, la question de l'équivalence de forêts d'horloges se pose donc. Une forme canonique de forêt a été définie [TPA95]. Un algorithme efficace pour trouver cette forme canonique a été développé. Il repose sur des manipulations préservant l'équivalence, prenant en compte l'ordre des variables résultant de la causalité, et combinées à des techniques BDD (Binary Decision Diagrams introduits par Bryant en 1986).

Le calcul dynamique s'appuie sur la représentation équationnelle d'un automate : les automates, leurs états, événements et trajectoires sont manipulés au travers des équations qui les représentent. Calculer des trajectoires d'états ou d'événements, des états atteignables, des projections de trajectoires, des états de deadlock, etc., s'effectue alors sur les coefficients des équations polynomiales. De manière similaire, des techniques de synthèse de contrôle ont été développées pour un système dynamique donné pour différents types d'objectifs de contrôle proposés par Manna et Pnueli, mais aussi pour des objectifs de contrôle portant sur la qualité de service.

La manipulation d'équations dans ${\cal F}_3$ est tout à fait similaire à la manipulation d'équations booléennes. Une variante de la technique BDD, appelée TDD (Ternary Decision Diagrams), a été développée pour réaliser ces calculs. Des expériences ont montré que le système formel Sigali qui en résulte peut effectuer en un temps raisonnable des preuves (ou de la synthèse de contrôleurs) sur des automates comportant plusieurs millions d'états atteignables.

Spécification et programmation synchrone / Sémantique synchrone / Langage Signal / Vérification et synthèse

Vérification et synthèse