Définition: Un système est vivace, si et seulement si pour tous les couples (x,y) tq Q(x,y)=0, P(x,y) est un état qui admet encore des transitions admissibles.
Propriétés de sécurité
Informellement,une propriété de sécurité décrit le fait que de "mauvaises choses" ne peuvent pas se produire. Dans notre cas, cette sorte de propriété couvre la classe des propriétés, décrivant un ensemble de bons états, qui restent invariants. La définition suivante rappelle la définition d'un ensemble d'états invariant.
Définition Un ensemble d'états E est invariant vis à vis d'un système dynamique polynomial, si et seulement si pour chaque état x de E et pour tout événement y admissible dans l'état x, l'état x'= P(x,y) appartient à E.
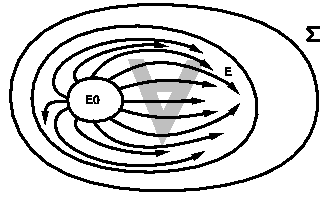
Un ensemble d'états est dit invariant sous-contrôle pour un système dynamique si et seulement si il est possible de le ``piloter'' en réalisant un choix sur les événements, de manière à rester dans l'ensemble des ``bons états''. Ainsi :
Définition
Un ensemble d'états E est invariant sous-contrôle vis à vis d'un système dynamique polynomial, si et seulement si pour chaque état x de E il existe un événement y admissible dans l'état x, tel que l'état x'= P(x,y) appartient à E.
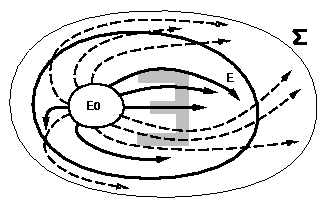
D'autres classes de propriétés peuvent se déduire à partir des propriétés d'invariance et d'invariance sous contrôle.
Propriété d'atteignabilité
Définition Un sous-ensemble F d'états est accessible pour un système dynamique, si et seulement si chaque état x de F peut être atteint à partir des états initiaux du système dynamique considéré (ie, il existe une trajectoire partant des états initiaux qui atteint x).
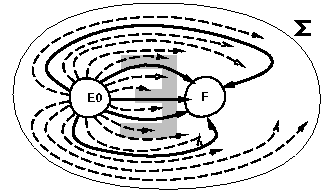
Propriété d'attractivité
Définition : Un ensemble d'états F est attractif vis à vis d'un autre ensemble d'états E , si et seulement si, chaque trajectoire du système initialisée dans un état de E atteint l'ensemble F.
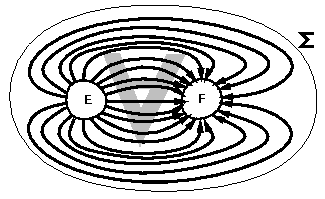
Nous avons donné un apercu des méthodes liées à la vérification de propriétés d'états pouvant être réalisées sur les systèmes dynamiques polynomiaux. Cette liste de propriétés n'est cependant pas exhaustive. Il est ainsi possible, en utilisant les mêmes méthodes algébriques d'exprimer des formules CTL , ainsi que des formules propositionelles de mu-calcul.
Webmaster : epatr_webmaster@irisa.fr
Last modified: Wed Mar 24 13:31:01 MET 1999