A ce jour, tous les objectifs de commande sont de types logiques. Des études sur les logiques temporelles ont été réalisées dans le but de pouvoir s'appuyer sur un langage permettant d'exprimer plus facilement ces objectifs de commande. Dans le cas des systèmes dynamiques polynomiaux, les objectifs de synthèse (comme d'ailleurs les propriétés liées à la vérification) sont tirés d'un catalogue de propriétés étudié par Pnueli, On y retrouve :

• La vivacité d'un système,
  
• l'invariance (sous contrôle) d'une propriété durant l'évolution d'un système,
  
• l'atteignabilité d'un ensemble d'états,
  
• l'attractivité d'un ensemble d'états finaux en partant d'un ensemble d'états initiaux.
  

Les systèmes dynamiques polynomiaux contrôlés

Par rapport aux systèmes dynamiques polynomiaux décrits dans la présentation des SDP, nous avons besoin d'introduire la notion d'événements contrôlables (resp. événements incontrôlables). Un système dynamique polynomial peut alors être réécrit comme suit :

où X représente toujours l'ensemble des variables d'états. Y et U, quant à eux, sont respectivement l'ensemble des variables incontrôlables et contrôlables. En simplifiant, les variables événements Y représentent les signaux reçus par des capteurs en provenance de l'extérieur, tandis que les variables événements U définissent les commandes du système qui doit être contrôlé. Un tel système est appelé système dynamique polynomial contrôlé.

Soient n, m, et p les dimensions respectives de X, Y et U. Les trajectoires du système dynamique polynomial contrôlé sont alors données par les suites (x_t, y_t, u_t) dans (F₃)ⁿ X (F₃)^m X (F₃)ⁿ telles que Q₀(X)=0 et, pour tout t,

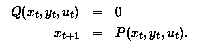
Les événements (y_t, u_t) comprennent une composante incontrôlable y_t et une composante contrôlable u_t . La composante y_t dépend uniquement de l'état courant x_t et aucune contrainte ne peut être induite sur cette composante. A contrario, la composante u_t est entièrement contrôlable. Il est possible de choisir n'importe quelle valeur admissible (ie, tel que Q(x_t, y_t, u_t) = 0 ). La valeur choisie détermine alors le nouvel état x_t+1 et influence par conséquent indirectement les valeurs possibles de y_t+1.

De manière à distinguer les deux composants d'un événement, un vecteur y appartenant à (F₃)^m sera appelé dans la suite un événement, tandis qu'un vecteur u appartenant à (F₃)^p aura pour nom commande. Ceci nous amène tout naturellement à une nouvelle notion d'amissibilité. Un événement y sera dit admissible dans un état x si et seulement si il existe une commande u telle que Q(x,y,u)=0; une telle commande est dite compatible avec y dans l'état x.

Le contrôleur

Le contrôle d'un tel système s'opère alors en sélectionnant en premier lieu un état initial particulier x₀ et en choisissant par la suite une séquence de commande particulière u₁, u_n, .....u_n, u_n+1, .. . Différentes statégies de contrôle peuvent alors être choisies pour déterminer la valeur des commandes possibles. Dans notre cas, nous ne considérerons pour l'instant que des objectifs de contrôle statique. Ainsi pour déterminer les valeurs d'une commande u à un instant t donné, il est juste nécessaire de connaître l'état courant du système x à cet instant et l'événement y qui s'est produit. Un tel contrôleur sera appelé controleur statique.

Formellement, un contrôleur statique est un système constitué de deux équations :

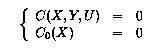
où l'équation C₀(X)=0 détermine les états initiaux que le contrôleur peut sélectionner. La deuxième équation (C(X,Y,U)=0) décrit les différents choix possibles pour les commandes. Quand le système contrôlé est dans l'état x et qu'un événement y se produit, toutes les commandes u telles que Q(x,y,u)=0 et C(x,y,u)=0 peuvent être choisies.

Le comportement global du système S composé avec le contrôleur est alors modélisé par le système suivant S_C:

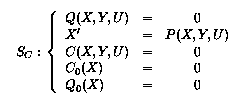
Cependant, tous les contrôleurs (C,C₀) ne constituent pas des contrôleurs acceptables. En premier lieu le système contrôlé S_C doit avoir des états initiaux. Ainsi, les équations Q₀(X) = 0 et C₀(X)=0 doivent avoir des solutions communes. De plus, en raison de l'incontrôlabilité des événements y, tous les événements y admissibles dans un état x pour le système S doivent également être admissibles pour le système contrôlable. Cette remarque nous amène à la définition d'un contrôleur acceptable.

Définition: un contrôleur acceptable pour un système S est donné par une équation de contrainte initiale C₀(X) = 0 et une équation de contrôle C(X,Y,U)=0 telles que :

• Les contraintes d'états intiales Q₀(X) = 0 et C₀(X)=0 doivent avoir des solutions communes.
  
• Pour tous les états x qui peuvent être atteints (potentiellement) durant l'évolution du système, tous les événements incontrôlables y admissibles dans l'état x pour le système intial S, le sont également pour le système contrôlé S_C.

Avant, de montrer les méthodes utilisées pour la synthèse de contrôleur, il est nécessaire de généraliser la notion d'invariance sous-contrôle

En partant d'un objectif de commande, formellement une fonction polynomiale, il est alors possible de synthétiser de manière automatique un contrôleur acceptable de manière à ce que le système dynamique polynomial contrôlé résultant vérifie l'objectif de commande.

Définition: Etant donné un système dynamique contrôlable, un sous-ensemble d'états E est U-invariant sous-contrôle si pour tout état x de E et tout événement y admissible dans x l'état, il existe une commande u telle que Q(x,y,u)=0 et x'=P(x,y,u) appartient à E.

Calcul du contrôleur

L'existence d'un contrôleur rendant invariant un ensemble d'états E est alors décrite par la propriété suivante:

Propriété : Étant donné un système dynamique contrôlable, S, et un ensemble d'états E, il existe un contrôleur statique acceptable rendant $E$ invariant si et seulement si:

• L'intersection de E et de l'ensemble des états solutions de Q₀ est non vide.
• E est U-invariant sous-contrôle pour le système dynamique S.

La prise en considération des conditions initiales nous dispense de nous préoccuper de l'action du contrôleur en dehors de E. La première condition indique simplement qu'il y a des états initiaux dans E et la notion d'invariance est celle s'appliquant à un système initialisé.

Si E n'est pas U-invariant sous-contrôle pour le système dynamique S, la solution consiste à calculer le plus grand sous-ensemble de E qui soit U-invariant sous-contrôle. Le contrôleur est alors calculé à partir de cet ensemble.

En utlisant des techniques similaires, il est possible de rendre accessible (ou attractif) un ensemble d'états.

Commande Optimale

Certains objectifs de contrôle peuvent se traduire par la question simple : est il possible de ``conduire'' le système considéré vers un ensemble donné d'états en garantissant certaines propriétés le long de la trajectoire? La théorie développée précédemment donne une réponse binaire : oui ou non. Lorsque la réponse est ``oui'',le contrôleur synthétisé permet de choisir les commandes adéquates pilotant le système de l'ensemble de départ vers l'ensemble d'arrivée. À ce niveau, une deuxième question peut alors se poser : quelle est la meilleur façon d'y arriver. La plus rapide, la moins couteuse, la plus sécuritaire.... Lorsque la réponse est ``non''; on peut parfois tolérer des écarts par rapport aux objectifs stricts, mais le problème est alors de les limiter. Il faut alors choisir un critère minimisant cet écart.

La théorie de la commande optimale peut fournir des réponses à ces questions. Le champ d'action de la commande optimale est donc extrêmement vaste. Il couvre le contrôle des tous les système dynamiques où une performance optimale est souhaitée. Le problème intrinsèque de la commande optimale est le choix du critère sur lequel l'optimalité va porter. Dans certains cas, ce critère est directement imposé par le système. Dans d'autres, au contraire, le choix du critère est (totalement) arbitraire et dépend fortement de la personne qui pose le problème. Bien souvent, on est amené à composer plusieurs critères entre eux.

Plus spécifiquement, dans le cadre des systèmes à événements discrets modélisés par des systèmes dynamiques polynomiaux, une étude entreprise en collaboration avec EdF, concernant la spécification du contrôle d'un poste de transformation électrique a mis en évidence le manque d'expressivité des propriétés logiques. Les différents problèmes posés par l'étude de ce poste ont en effet permis de dégager différents types d'objectifs de contrôle impossibles à synthétiser en utilisant les méthodes actuellement à notre disposition (vivacité, invariance, atteignabilité, attractivité). Ces objectifs de commande sont de natures différentes et portent plus sur les moyens à utiliser pour atteindre un objectif logique, plutôt que sur le but à atteindre. Il est apparu qu'il était possible d'exprimer ces objectifs de contrôle en ordonnant les états du système suivant une certaine relation d'ordre. Dans ce cas, le contrôle revient à choisir, pour un état donné, la commande faisant évoluer le système vers l'état considéré comme étant le meilleur pour la relation d'ordre. Nous parlerons alors d'objectif d'optimalité statique, pour les objectifs de contrôle exprimés comme une relation d'ordre entre états et de commande optimale statique. Les objectifs d'optimalité statiques peuvent également être composés avec des objectifs de contrôle logiques de manière à obtenir potentiellement des lois de contrôle (expression des commandes en fonction des entrées non controlables et des états).

Cependant, la commande optimale statique n'autorise que le contrôle à un pas. Elle ne réalise en effet qu'un optimum local (à un instant t donné de l'évolution du système, la commande choisie sera la meilleure). Il apparaît donc intéressant d'étendre cette notion d'optimalité sur une trajectoire bornée du système. On parlera alors de commande optimale dynamique (en corrélation avec la programmation dynamique).

Au contraire de la commande optimale statique, la commande optimale dynamique permet d'obtenir un critère d'optimalité global. Le problème de la commande optimale consiste alors en la synthèse d'un contrôleur capable de choisir les valeurs d'une séquence de commandes faisant évoluer le système d'un ensemble d'états initiaux vers un ensemble d'états finaux tout en minimisant une fonction de coût sur les états où les événements, donnée à priori. Les différents résultats sur ce sujets ont été décrits par Passino & Ansalkis, et Sengupta & Lafortune.

1. Commande optimale statique

   Les objectifs de commande étaient jusqu'à présent d'ordre logique. L'étude entreprise sur le poste de transformation électrique EdF a permis de dégager des types d'objectifs de commande de natures différentes. Au contraire des objectifs de contrôle d'ordre logique, l'objectif d'optimalité porte plus sur la priorité et la qualité de service par l'intégration d'un aspect quantitatif. Par exemple dans le poste de transformation électrique EdF, apparaissent des ordres de priorité quant à l'ouverture des disjoncteurs, ainsi que la nécessité d'assurer la distribution à un maximum d'usagers. La formalisation de ces objectifs est réalisée en introduisant la notion de relation d'ordre (ou de pré-ordre) sur les états du système. Le contrôle revient alors à choisir parmi les solutions admissibles les solutions respectant au mieux la relation d'ordre. De plus, les contrôleur résultant d'un objectif de commande logique ne sont, en général, pas déterministe, dans le sens où, pour un état donné et un événement incontrôlable produit (ou reçu), différents événements incontrôlables peuvent être choisis. Il est alors envisageable de composer des objectifs de commande optimaux avec les objectifs de commande logiques, de manière à réduire le comportement du système et atteindre éventuellement une loi de contrôle fonctionnelle. Les degrés de liberté laissés par le contrôleur indéterministe sont ainsi mis à profit pour affiner la loi de commande. Suivant la nature du problème, il sera parfois plus facile d'exprimer ces nouveaux objectifs de commande en terme de priorités. Ceci amène naturellement à introduire des relations d'ordre. Dans certains cas, il sera possible d'affecter un coût entier aux différentes solutions et de choisir celle de coût minimal. Ces fonctions de coûts sont alors traduites sous forme d'équations polynomiales dans Z/3Z, de manière à se ramener aux cas précédents

   Parmi les objectifs d'optimalité statiques généraux, synthétisables, on peut trouver :

   La maximisation du degré de liberté d'un système
   La maximisation du nombre de variables d'états actives
   La stabilisation d'un système
   

2. Commande optimale dynamique

   Depuis quelques années, suite à des travaux sur la stabilisation et le contrôle des systèmes à événements discrets partiellement observables, les recherches sur les systèmes à événements discrets se sont orientés vers l'introduction de la commande optimale. Le problème de la commande optimale consiste en la synthèse d'un contrôleur capable de choisir les valeurs d'une séquence de commandes faisant évoluer le système d'un ensemble d'états initiaux vers un ensemble d'états finaux tout en minimisant une fonction de coût sur les états où les événements, donnée à priori.

   Nous avons donc développé une méthode de synthèse de contrôleur permettant de minimiser le coût d'une suite finie de transitions afin de faire évoluer le système d'un ensemble d'états initiaux vers un ensemble d'états finaux. Le modèle utilisé pour représenter notre système est celui des systèmes à événements discrets polynomiaux. Dans un premier temps, tous les événements sont contrôlables (Il n'y a donc pas de perturbation). À chaque transition, ainsi qu'à chaque état, est associé un coût positif . Les algorithmes développés se basent sur des études réalisées dans le domaine de la programmation dynamique.

   Une première phase consiste à affecter à chaque état du système un coût correspondant au coût minimal qu'il faut pour aller de cet état à un des états finaux. La deuxième phase réalise le calcul du contrôleur. Le but de celui-ci est de choisir, dans un état donné, entre les différentes commandes admissibles, la commande faisant transiter le système dans un état tel que le coût de cet état ajouté au coût de la commande correspondante soit minimal.

   Le cas avec perturbation (où entrées incontrôlables) est quasi identique mais avec une technique de ``min-max'' au lieu de ``min''. En effet, comme il n'est pas possible d'empêcher un événement incontrôlable de se produire, dans un état donné, il faut considérer que le pire peut se produire (ie, la transition admissible de coût maximum s'effectue). Pour un état x donné, on affecte donc aux états permettant d'accéder à x en une transition un coût égal au maximum du coût des transitions incontrôlables additionné au coût minimum des transitions contrôlables qui sont admissibles une fois la transition incontrôlable choisie, ainsi que le coût déjà calculé de l'état ainsi atteint. Le principe d'optimalité revient donc à choisir la meilleure trajectoire possible parmi les trajectoires les pires.