EP-ATR

Spécification et programmation synchrone / Sémantique synchrone / Langage Signal / Vérification et synthèse

Les usages différents des termes synchrone et asynchrone selon les contextes dans lesquels ils apparaissent font qu'il nous semble nécessaire de préciser, autant que possible, ce qui constitue l'essence même du paradigme synchrone. Les points suivants apparaissent comme caractéristiques de l'approche synchrone :

Le comportement des programmes synchrones progresse via une suite infinie d'actions composées.
Chaque action composée est constituée d'un nombre borné d'actions élémentaires, pour les langages Esterel, Lustre et Signal.

À l'intérieur d'une action composée, les décisions peuvent être prises sur la base de l'absence de certains événements, comme il apparaît sur l'exemple des trois instructions suivantes, issues respectivement de Esterel, Lustre, et Signal :

present x else `stat'	l'action `stat` est exécutée en l'absence du signal `x`.

`y = current x`	en l'absence d'occurrence du signal `x`,
	`y` prend la valeur de la dernière occurrence de `x`.

`y := x default z`	en l'absence d'occurrence des signaux `x` et `z`,
	`y` est absent,
	sinon en l'absence d'occurrence du signal `x`,
	`y` prend la valeur de `z`.

Lorsqu'elle est définie, la composition parallèle de deux programmes s'exprime toujours par la composition des couples d'actions composées qui leur sont respectivement associées, elle-même obtenue par la conjonction de leurs actions élémentaires respectives.

Pour ce qui concerne la spécification de programmes (ou de propriétés), la règle ci-dessus est clairement la bonne définition de la composition parallèle.

S'il s'agit également de programmation, la nécessité que cette définition soit compatible avec une sémantique opérationnelle complique largement la condition «lorsqu'elle est définie».

Sémantique synchrone

La sémantique fonctionnelle d'un programme Signal est décrite comme l'ensemble des suites admissibles de valuations des variables de ce programme dans un domaine de valeurs complété par la notation d'absence d'occurrence [PLG91b].

Considérant :

A, un ensemble de variables,
D, un domaine de valeurs incluant les booléens,
$\bot$ , n'appartenant pas à D,

une trace T sur A₁ $\subset$ A est une fonction T : $\mathbb{N}$ $\rightarrow$ A₁ $\rightarrow$ (D $\cup$ { $\bot$ }).

Pour tout k $\in$ $\mathbb{N}$ , un événement sur A₁ est une valuation T(k) : une trace est une suite d'événements. On appelle événement nul l'événement dans lequel chaque valeur est égale à $\bot$ .

Pour toute trace T, il existe une trace F unique appelée flot, notée flot(T), dont la sous-suite des événements non nuls est égale à celle de T et initiale dans F. La projection $\pi_{A_2}^{}$ (F) sur un sous-ensemble A₂ $\subset$ A₁ d'un flot F, défini sur A₁, est le flot flot(T) pour T trace des restrictions des événements de F à A₂.

Un processus P sur A₁ est alors défini comme un ensemble de flots sur A₁. L'union de l'ensemble des processus sur A_i $\subset$ Aest noté ${\cal P}_A$ .

Étant donné P₁ et P₂ deux processus définis respectivement sur des ensembles de variables A₁ et A₂, leur composition, notée P₁| P₂, est l'ensemble des flots F définis sur A₁ $\cup$ A₂tels que $\pi_{A_1}^{}$ (F) $\in$ P₁ et $\pi_{A_2}^{}$ (F) $\in$ P₂. La composition de deux processus P₁ et P₂ est ainsi définie par l'ensemble de tous les flots respectant, en particulier sur les variables communes, l'ensemble des contraintes imposées respectivement par P₁ et P₂.

Soit $\mbox{${\bf 1}_{{\cal P}}$}$ le processus ayant comme seul élément la trace (unique) sur l'ensemble vide de variables. On montre alors que $({\cal P}_A,\mbox{${\bf 1}_{{\cal P}}$ },\vert)$ est un monoïde commutatif (cette propriété rend possibles les transformations de programmes mentionnées dans la section suivante:

(P₁| P₂)| P₃ = P₁|(P₂| P₃)

P₁| P₂ = P₂| P₁

P| $\displaystyle \mbox{${\bf 1}_{{\cal P}}$ }$ = P

De plus, pour tout A₁ $\subset$ A, les processus ${\bf0}_{{\cal P}}$

Langage Signal

Un programme Signal [PLG91] spécifie un système temps réel au moyen d'un système d'équations dynamiques sur des signaux. Les systèmes d'équations peuvent être organisés de manière hiérarchique en sous-systèmes (ou processus). Un signal est une suite de valeurs à laquelle est associée une horloge, qui définit l'ensemble discret des instants auxquels ces valeurs sont présentes (différentes de $\bot$ ). Les horloges ne sont pas nécessairement reliées entre elles par des fréquences d'échantillonnage fixes : elles peuvent avoir des occurrences dépendant de données locales ou d'événements externes (comme des interruptions, par exemple).

Le langage Signal est construit sur un petit nombre de primitives, dont la sémantique est donnée en termes de processus tels que décrits ci-dessus. Les autres opérateurs de Signal sont définis en terme de ces primitives, et le langage complet fournit les constructions adéquates pour une programmation modulaire.

Pour un flot F, une variable X et un entier t on note, lorsqu'il n'y a pas de confusion possible, X_t la valeur F(t)(X) portée par X en t dans le flot F. On note par le même symbole une variable ou une fonction dans les domaines syntaxique et sémantique. Dans le tableau ci-dessous, on omet les événements nuls (qui, rappelons-le, terminent les flots ayant un nombre fini d'événements non nuls).

Le noyau de Signal se compose des primitives suivantes :

Fonctions ou relations étendues aux suites :
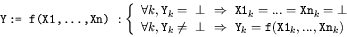
$\begin{displaymath}\mbox{{\tt Y := f(X1,...,Xn)}}~: \left\{ \begin{array}{l} \fo... ...t Y}_k = {\tt f}({\tt X1}_k,...,{\tt Xn}_k) \end{array}\right. \end{displaymath}$
Retard (registre à décalage) :
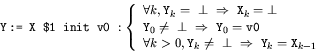
$\begin{displaymath}\mbox{{\tt Y := X \$1 init v0}}~: \left\{ \begin{array}{l} \f... ...bot\ \Rightarrow\ {\tt Y}_k = {\tt X}_{k-1} \end{array}\right. \end{displaymath}$
Extraction sur condition booléenne :
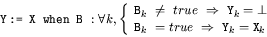
$\begin{displaymath}\mbox{{\tt Y := X when B}}~: \forall k, \left\{ \begin{array}... ... = true\ \Rightarrow\ {\tt Y}_k = {\tt X}_k \end{array}\right. \end{displaymath}$
Mélange avec priorité :
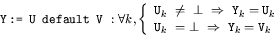
$\begin{displaymath}\mbox{{\tt Y := U default V}}~: \forall k, \left\{ \begin{arr... ... = \bot\ \Rightarrow\ {\tt Y}_k = {\tt V}_k \end{array}\right. \end{displaymath}$

La composition de deux processus P| Q se traduit directement en la composition des ensembles de flots associés à chacun d'eux.

La restriction de visibilité de X, P / X est la projection de l'ensemble des flots associés à P sur l'ensemble des variables obtenu en enlevant X à celles de P.

Comme on peut le voir pour les primitives, chaque signal a sa propre référence temporelle (son «horloge», ou ensemble des instants où il est différent de $\bot$ ). Par exemple, les deux premières primitives sont monocadencées : elles imposent que tous les signaux impliqués aient la même horloge. En revanche, dans la troisième et la quatrième primitives, les différents signaux peuvent avoir des horloges différentes. L'horloge d'un programme Signal est alors la borne supérieure de toutes les horloges des différents signaux du programme (les instants du programme sont les instants de l'un au moins de ces signaux).

Le compilateur de Signal consiste principalement en un système formel capable de raisonner sur les horloges des signaux, la logique, et les graphes de dépendance. En particulier, le calcul d'horloges [TPA95] et le calcul de dépendances fournissent une synthèse de la synchronisation globale du programme à partir de la spécification des synchronisations locales (qui sont données par les équations Signal), ainsi qu'une synthèse de l'ordonnancement global des calculs spécifiés. Des contradictions et des inconsistances peuvent être détectées au cours de ces calculs.

On peut toujours ramener un programme P comportant des variables locales à un programme, égal à P, de la forme Q/A1/.../An où Q est une composition de processus élémentaires sans restriction de visibilité (i.e., sans R/A). Un principe général de transformation de programmes que nous appliquons (dans un but de vérification, pour aller vers la mise en oeuvre, pour calculer des abstractions de comportement) est alors de définir des homomorphismes $\mbox{${\cal T}_i$}$ sur les programmes Signal, tels que Q est égal à la composition de ses transformés par $\mbox{${\cal T}_i$}$ . Grâce aux propriétés du monoïde commutatif, la transformation qui à Q associe cette composition est elle-même un homorphisme. On sépare ainsi un programme en différentes parties sur lesquelles seront alors appliqués des traitements spécifiques.

dernière mise à jour :
	english version		epatr_webmaster@irisa.fr		©copyright