Fractals de Rauzy: propriétés
Le vrai fractal de Rauzy
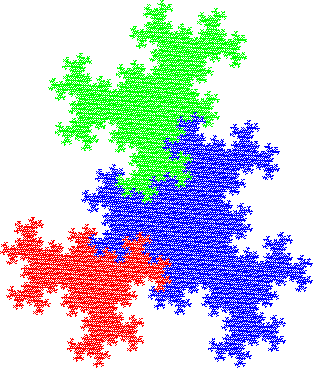
Commençons avec le fractal de Rauzy, le vrai, le seul, associé à la substitution de Tribonacci
encore appelée substitution de Rauzy : s(1)=12, s(2)=13, s(3)=1.
![[fractal
de Rauzy de la substitution de tribonacci]](../people/asiegel/Dessins/fractal_rauzy.gif)
Parmi ses nombreuses propriétés, citons:
- Stable par un échange de morceaux : si on pousse le bleu vers la droite, et si on remonte le rouge vers
la gauche, tout en descendant le vert vers la gauche, on obtient exactement le même ensemble.

- Compact.
- Autosimilaire : le vert est une copie du bleu
qui a été rétrécie puis tournée. Le
rouge est une copie du vert qui a été rétrécie dans les mêmes
proportions et tournée du même anglportions et tournée du même angle.

- Connexe, simplement connexe : le dessin ne peut pas etre coupé en deux et ne contient
pas de trou.
- pavage périodique : si on décale le dessin dans deux directions données, on recouvre
exactement toute la page, sans qu'autre chose que les bords des figures ne se recouvrent....

- pavage auto-similaire : on peut positionner les pièces du fractal selon un arrangement tel qu'en décomposant chaque pièce avec les règles d'autosimilarité qui gouvernent le fractal, on retrouve exactement le même pavage.

- Engendre un pavage périodique de l'espace : prenez le fractal de Rauzy (qui est plan), posez le sur un feuille
de papier dans l'espace, remontez chacune des couleurs d'une hauteur déterminée... On obtient un joli
volume dans l'espace, cylindrique ayant pour base le fractal de Rauzy.
Si on recopie ce volume vers le haut et sur les côtés, on obtient un recouvrement
régulier de tout l'espace.


Généralisation
Pour toute substitution de type Pisot et unimodulaire, qui vérifie en plus une condition
particulière (la condition de coincidences) -- mais pour l'instant on
ne connait aucune substitution de ce type sans coincidences -- on peut construire
un ensemble du même genre encore appelé fractal de Rauzy de la substitution. Des
exemples sont les suivants :








On connait un certain nombre de propriétés des fractals de Rauzy :
- Ils sont tous compacts.
- Ils sont tous autosimilaires : on peut découper l'ensemble en plusieurs bouts qui
sont chacun constitués de certains de ces mêmes bouts préalablement rétrécis et tournés.
- Ils ne sontpas tous connexes : le troisième exemple peut-être clairement découpé en deux
bouts disjoints. Par contre les deux premiers exemples sont connexes. Il existe des critères pour
savoir si un fractal de Rauzy est connexe.
- Ils ne sont pas tous simplement connexes : le premier exemple est plein de trous. Là encore, des critères existent.
- On a un critère pour savoir si un fractal de Rauzy engendre un pavage périodique. Toutes
les substitutions testées à ce jour le vérifie. Ainsi, pour le premier exemple, si on le décale correctement,
les trous se bouchent exactement sans se recouvrir.

- Pour les fractals qui engendrent un pavage périodique, on peut les remonter en cylindre comme le
fractal de Rauzy (en remontant chacune des couleurs d'une hauteur donnée). On obtient alors un
volume qui, décalé régulièrement, rempli tout l'espace, et fournit donc un pavage périodique de l'espace. Mais attention, ce volume peut avoir
une forme surprenante : dans l'exemple ci-contre, on va obtenir un gruyère. Ce qui n'empêche
pas les vides du gruyère de se combler sans se superposer lorsqu'on déplace le gruyère régulièrement.
Pour en savoir plus
Question de recherches associées
- Théorie ergodique: tous les systèmes substitutifs Pisot unitaire ont-ils spectre purement discret ?
- Géométrie: Construire des partitions de Markov pour des
endomorphismes du tore qui ne sont pas de type Pisot.
- Topologie : Propriétés géométriques des fractals de Rauzy
- Systèmes de numération : exploitation des fractals pour obtenir des informations sur les numérations en base non entière.
- Analyse diophantienne ; Fractions continues généralisées.
Considerer une suite de substitutions pour approximer des vecteurs,
éventuellement non algébriques.
- Géométrie discrète et substitution multi-dimensionnelles : Approximer/reconnaitre des plans discrets
- Morphismes de groupes libres: Représenter les morphismes de
groupes libres iwip et en déduire une mesure sur l'espace des
laminations d'un groupe libre.
Etat des lieux, 2001
Systèmes substitutifs
Une substitution est à la base un objet qui s'applique
sur des lettres, mais on peut canoniquement étendre
sa définition et appliquer
une substitution à tout mot infini (unilatéral comme
bilatéral) en remplaçant chacune des lettres
du mot par son image par la substitution.
Etant donné une substitution sur $d$ lettre,
un mot infini bilatéral sur l'alphabet $\{1, \dots, d\}$
est appelé point périodique de la substitution
si une itération finie de la substitution sur ce mot
redonne le même mot. Si la substitution
mélange suffisamment les lettres (condition de primitivité), les points périodiques d'une substitution
ont même ensemble de sous-mots finis ou facteurs. En rassemblant
dans un sous-ensemble de $\{ 1, \dots, d\}^{\mathbb Z}$
tous les mots bilatéraux qui ont
ce même ensemble de facteurs, on obtient
un ensemble compact qui est stable par le
décalage sur $\{ 1, \dots, d\}^{\mathbb Z}$. Ce système dynamique symbolique est minimal
et uniquement ergodique.
Les systèmes ainsi obtenus, appelés systèmes substitutifs,
présentent des propriétés d'autosimilarité
du fait qu'ils
sont engendrés par des points pét qu'ils
sont engendrés par des points pé\-rio\-di\-ques pour la substitution.
On retrouve ainsi ces systèmes lorsqu'on code l'action
de diverses transformations géométriques ou arithmétiques
qui ont elles-mêmes des propriétés d'auto-induction.
Le premier exemple significatif est la substitution
de Prouhet-Thue-Morse définie par $\sigma(1)=12$, $\sigma(2) =21$.
En 1907, Thue
étudia la combinatoire du point fixe de cette substitution
dans le cadre de l'étude de suites symboliques sans facteur carré.
En 1921, M. Morse
a utilisé cette substitution
pour construire des géodé\-siques récurrentes
non fermées sur des surfaces à courbure négative. Plus
tard, il a été prouvé que le système symbolique associé
à cette substitution est une extension à deux points
de l'odomètre dyadique.
Un certain nombre
de résultats ont été obtenus sur la relation existant entre
certains systèmes substitutifs et des échanges de morceaux
tels que des intervalles du cercles ou des parties autosimilaires
d'espaces euclidiens. G. Rauzy (19981), G. Rauzy et P. Arnoux (1992), B. Solomyak (1992), M. Boshernitzan et
I. Kornfeld (1995), S. Ferenczi (1995),
C. Holton et L. Zamboni (1998), P. Arnoux et S. Ito (1998) ont ainsi
prouvé des résultats dans ce domaine.
Entre autres exemples, la substitution
de Fibonacci est définie par $\sigma(1)=12$, $\sigma(2)=1$.
Cette substitution
a des propriétés combinatoires et diophantiennes
très particulièet diophantiennes
très particulières : elle engendre
un système qui d'une part code l'action d'une translation
sur le tore de dimension 1, d'autre part contient des mots
dont la complexité combinatoire est minimale
parmi les suites non ultimement périodiques.
Le fractal de Rauzy
En 1981 G. Rauzy a généralisé les propriétés
dynamiques de la substitution de Fibonacci à
une substitution sur 3 lettres appelée substitution
de Tribonacci :
$\sigma(1)=12$, $\sigma(2)=13$, $\sigma(3)=1$.
Notons qu'à toute substitution $\sigma$ sur $d$ lettres
est associée une matrice $d\times d$,
dont le coefficient d'indice $(i,j)$ est le nombre de $i$ qui apparaissent
dans $\sigma(j)$. De la même manière, tout mot fini sur $d$ lettres
est linéarisable en un vecteur de ${\mathbb N}^d$
constitué du nombre d'occurrences dans le mot de chaque
lettre de l'alphabet.
La matrice de la substitution apparaît alors comme la linéarisation
de la substitution.
La matrice de la substitution
de Tribonacci $\sigma$ a pour polynôme caractéristique
$X^3 - X^2 - X -1$, ses valeurs propres étant un réel
$\beta > 1$ et deux complexes
conjugués $\alpha$, $\overli
conjugués $\alpha$, $\overline{\alpha}$. Le nombre
$\alpha$ est appelé nombre de Tribonacci.
En particulier, cette matrice admet dans ${\mathbb R}^3$ une droite dilatante
et un plan contractant. On peut représenter le point fixe
de $\sigma$ en une ligne brisée de ${\mathbb R}^3$
en remplaçant chaque des lettres du
point fixe
par le vecteur de base de ${\mathbb R}^3$ correspondant. Cette ligne
brisée
a la propriété de rester à distance bornée de la direction
dilatante de la matrice, s'enroulant autour
de cette droite. L'adhérence des projections des sommets
de la ligne brisée sur le plan contractant
parallèlement à la droite dilatante constitue
un sous-ensemble compact ${\mathcal R}$ du plan contractant de la matrice,
appelé
fractal de Rauzy.
Trois sous-ensembles du fractal de Rauzy se distinguent :
pour chaque lettre, on appelle cylindre
l'adhé\-ren\-ce des projections des
sommets de la ligne brisée qui appartiennent
au vecteur canonique correspondant à la lettre.
Ces cylindres constituent un recouvrement de
${\mathcal R}$, et Rauzy montrent que leurs intersections
sont de mesure nulles. Les cylindres pavent donc le
fractal de Rauzy.
De plus, sur la ligne brisée, on se déplace de sommet en sommet
en se déplacer par un des 3 vecteurs de la base canonique.
Ainsi, dans le plan contractant, on peut translater chaque
cylindrpeut translater chaque
cylindre par le projeté du vecteur canonique correspondant,
tout en restant dans ${\mathcal R}$. On définit
ainsi échange de morceaux dans le fractal de Rauzy.
Il est naturel de coder, dans la partition
définie par les cylindres, l'action de cet échange de
morceaux sur ${\mathcal R}$. Rauzy montre que l'application
de codage est injective en mesure, surjective dans
le système substitutif associé à la substitution
de Tribonacci, et réalise ainsi un isomorphisme
mesurable entre l'échange de morceaux
de ${\mathcal R}$ avec le décalage sur le système
substitutif.
L'autosimilarité du système substitutif se transmet
graphiquement sur l'ensemble
${\mathcal R}$ par le fait que chacun des sous-ensembles
de ${\mathcal R}$ n'est rien d'autre que la copie de ${\mathcal R}$
multipliée par un des complexes $\alpha$, $\alpha^2$ ou $\alpha^3$.
De plus, on peut quotienter ${\mathbb C}$ par un réseau
de telle façon que l'échange de morceaux
sur ${\mathcal R}$ se quotiente en une translation sur un tore,
et ce passage au quotient est neutre, au sens qu'il
est injectif en mesure. Ceci signifie plus graphiquement
que les décalés de ${\mathcal R}$ selon un réseau
donné ne s'intersectent pas. Par le théorème
de Kronecker, ces décalés recouvrent
${\mathbb C}$.
Notons pour obtenir ces résultats,
Rauzy montre que le fractal de Rauzy peut aussi être
défini numérique\-ment
comme l'ensemble des sommes de séries en $\alpha$ dont les
digits sont toutes les suites de $0,1$ qui ne contiennent pas
trois 1 consécutifs :
${\mathcal R} = \{ \sum_{i \geq 0} \varepsilon_i \, \alpha^i;
\, \varepsilon_i=0,1; \, \varepsilon_i\varepsilon_{i+1}\varepsilon_{i+2}
=0 \} \subset {\mathbb C}$.
L'utilisation couplée
de la dynamique, des propriétés d'autosimilarité
et de la théorie des nombres
permet finalement de montrer le résultat suivant, qui s'énonce
de plusieurs manières :
-
géométriquement : le fractal de de Rauzy engendre
un pavage périodique et auto-similaire de ${\mathbb C}$,
-
dynamiquement : le système dynamique engendré
par la substitution de Tribonacci est mesurablement isomorphe
à une rotation sur un tore,
-
spectralement : ce système
dynamique est à spectre purement discret.
On peut se demander si cette propriété est
généralisable à une classe de substitutions : quelles
sont les substitutions qui engendrent un pavage périodique
autosimilaire ? Autrement dit, lesquelles codent l'action d'une rotation
sur un tore ? D'un point de vue spectral, de telles substitutions
engendrent un système dynamique qui est à spectre purement discret.
Une forme générale de la question des pavages est alors :
quelles sont les substitutions qui engendrent un système
symbolique dont le spectre est discret ?
Théorie spectrale des systèmes substitutifs
Une réponse précise a été donnée à cette dernière question
pour les substitutions de longueur constante,
durant les années 1960-1970, avec les travaux de
T. Kamae, J. C. Martin et F. M. Dekking en particulier. On sait ainsi
que le facteur équicontinu maximal des systèmes substitutifs
de longueur constante $l$ est une translation sur le
produit direct du groupe
des entiers $l$-adiques ${\mathbb Z}_l$ et d'un groupe fini.
Il y a de plus un isomorphisme mesurable entre
un système substitutif de longueur
constante et son facteur équicontinu maximal si et seulement
si la substitution vérifie une condition combinatoire simple
dite de coincidences. Il existe des exemples élémentaires
comme la substitution de Morse qui ne vérifient pas cette
condition.
En longueur non constante, G. Rauzy a abordé cette
question avec l'étude précédemment détaillée
du système associé à la substitution
de Tribonacci.
B. Host a ensuite fait un pas significatif
en montrant que les fonctions propres des syue les fonctions propres des systèmes substitutifs
primitifs sont continues. Ainsi, très opportunément, les deux principales
classifications dynamiques que sont la classification
par isomorphisme mesurable et celle par isomorphisme topologique
sont équivalentes dans le cas des systèmes substitutifs primitifs.
La situation est donc notablement plus simple
que dans le cas des automorphismes
du tore classifiés par Adler et Weiss.
B. Host donne aussi une caractérisation
des valeurs propres des systèmes substitutifs.
En particulier, le spectre d'un système substitutif
se divise en deux parties, la première, d'origine
arithmétique, et la seconde, d'origine plus
combinatoire, étant aussi liée aux mots de retour associés
au point fixe de la substitution.
Concrètement, ces travaux fournissent
un cadre pour les espaces dans lesquels une représentation
a une chance d'exister : si un système substitutif
est isomorphe à une rotation sur un groupe compact,
cette rotation doit ``contenir'' toutes les valeurs
propres du système. Ainsi, le groupe compact
sera un tore de dimension $n$ si le spectre du système
est purement irrationnel et de rang $n$, il contiendra
des groupes finis si le spectre contient des rationnels,
des groupes $p$-adiques s'il y
a suffisamment de valeurs propres rationnelles comme dans
le cas de la longueur constante, voire des solénoides.
Géométriquement, si le système substitutif code
de manière injective tif code
de manière injective une action dans un espace
donné, cet espace doit contenir des composantes
réelles ou $p$-adiques en fonction de l'irrationnalité
du spectre. Ces travaux fournissent de plus
un réseau susceptible de générer le pavage
périodique de l'espace.
A l'intérieur de ce cadre, on peut
maintenant chercher une bonne représentation
des systèmes substitutifs généralisant le fractal
de Rauzy, c'est à dire un ensemble à structure
autosimilaire et une action sur cet ensemble
dont le codage donne le système substitutif.
Définition générale des fractals de Rauzy
On peut construire un fractal de Rauzy pour toute substitution dont la matrice
a un espace dilatant de dimension 1 et telle que la
ligne brisée correspondant à un de ses points fixes
reste à distance bornée de cette droite dilatante. Ceci est
assuré dans le cas où toutes les valeurs
propres de la matrice sauf une sont de module inférieur à 1 strictement.
Ainsi, la valeur propre dominante de la matrice est un nombre
de Pisot, et une telle substitution est dite de type Pisot.
Pour toute substitution de type Pisot, on appelle fractal
de Rauzy de la substitution
la projection dans l'hyperplan
contractant de la matrice de la substitution, des sommets
du linéarisé du point fixe de la substitution. Le fractal de Rauzy est
alors recouvert par $d$ cylindres (où $d$ est le nombre de lettres de
l'alphabet)
correspondant à chacun des vecteurs de la base canonique. Exemple 1.
Exemple 2.
Exemple 3.
Sur le fractal
est défini un pseudo-échange de morceaux :
chacun des cylindres peut-être translaté tout
en restant dans le fractal de Rauzy, par
la projection dans l'espace contractant du vecteur de base correspondant.
Les $d$ cylindres constituent par construction un recouvrement du fractal
de Rauzy,
mais rien ne permet d'affirmer qu'il s'agit
d'une partition mesurable, c'est-à-dire que
les cylindres s'intersectent sur un ensemble de mesure nulle.
Pour cela, le déterminant
de la matrice de la substitution doit être
$\pm 1$ : la substitution est alors
dite unimodulaire. Cette condition est nécessaire
car les systèmes non unimodulaires admettent une composante
spectrale rationnelle. On ne sait pas si elle est suffisante.
Les travaux de B. Host ont permis
de mettre en évidence une condition suffisante
sur les substitutions unimodulaires de type Pisot
sur 2 lettres pour a Pisot
sur 2 lettres pour avoir une partition :
cette condition purement combinatoire, dite de coïncidences,
généralise la condition
de F. M. Dekking sur les substitutions
de longueur constante et
signifie que les points périodiques de la substitution
ont suffisamment de parties communes. P. Arnoux et S. Ito
ont généralisé cette condition pour les substitutions de type Pisot
unimodulaires sur plus de 2 lettres (1998). Sous cette condition,
la première propriété du fractal de Rauzy se généralise :
pour toute substitution sur $d$ lettres, unimodulaire, de type Pisot
et vérifiant la condition de coïncidences, le fractal
de Rauzy associé à la substitution admet une partition
mesurable en $d$ cylindres et est associé à un échange
de morceaux tel que le codage de l'action de l'échange de morceaux
selon les cylindres donne exactement le système symbolique associé
à la substitution.
Le système substitutif
est ainsi conjugué en mesure à un échange de morceaux dans le
fractal de Rauzy de la substitution.
Notons qu'on ne connaît aucun exemple de substitution
de type Pisot sans coïncidences.
De plus, le fait que les $d$ cylindres constituent une partition
du fractal de Rauzy implique que le fractal de Rauzy a encore
une structure autosimilaire.
Condition de pavage ? Système à spectre discret ?
La question qui se pose alors est la généralisation
du fait que
le fractal de Rauzy associé à la substitution de Tribonacci
engendre un pavage périodique du plan. On peut toujours quotienter le fractal de Rauzy d'une substitution
unimodulaire, de type Pisot et avec coïncidences,
par un réseau tel que les vecteurs de l'échange
de morceaux soient égaux par passage au quotient.
Le système substitutif est alors représenté
par une rotation sur un tore, dont la théorie spectrale
nous dit, sous une condition
combinatoire d' absence de cobords non triviaux,
qu'elle est le facteur
équicontinu maximal du système substitutif (B. Host, A. Livshits). En
particulier, ceci signifie que les décalés du fractal de Rauzy d'une
substitution par le réseau précédent recouvrent l'espace. Ces décalés
pavent alors l'espace si et seulement si le système substitutif
est à spectre discret, mais la théorie spectrale
des substitutions est très pauvre sur ce sujet :
les travaux de B. Host, A. Livshits
puis M. Hollander ont montré que sur deux lettres,
la condition de coïncidences est encore suffisante
pour que le spectre soit discret.
B. Solomyak, utilisant les $\beta$-développements, a trouvé
des exemples de substitutions Pisot sur titutions Pisot sur plus de 2
lettres qui sont
à spectre discret. P. Arnoux et S. Ito ont donné
une condition suffisante pour que le spectre soit discret, mais
difficile à vérifier. En particulier, il a été impossible
de prouver que la condition de coïncidences est encore suffisante
pour qu'il y ait pavage/spectre discret.
La question reste donc ouverte de savoir quels sont les systèmes
substitutifs unimodulaires de type Pisot sur plus de 2 lettres qui
sont à spectre discret. Excepté pour la substitution
de Tribonacci et ses généralisations
naturelles, très peu d'exemples et aucun contre-exemples ne sont
connus. Graphiquement, tous les exemples
semblent vérifier cette condition. On dispose depuis Barge et Kwaplisz d'une condition équivalente d'un point de vue combinatoire, cependant, on ne sait pas encore montrer que toutes les substitutions la vérifient, mis-à-part certaines familles de beta-substitutions.
Cette question concerne aussi
les systèmes de type Pisot non unimodulaires : à part pour les
substitutions sur 2 lettres (où la condition
de coïncidences répond à la question), aucun résultat
n'est connu sur le caractère discret ou non des
systèmes non unimodulaires. Seul leur spectre est partiellement
connu. Encore plus généralement, quelle est la nature des systèmes
substitutifs qui ne sont pas de type Pisot ? A-t-on encore parfois
affaire à des rotations ? A des échanges de morceaux ?
Très peu de résultats existent sur ce sujet, la plupart
provenant de la théorie spectrale n'étant pas explicites.