




Next: Experimental Results and Evaluation
Up: Using Neural Networks for
Previous: Introduction
Contents
Index
Our Method
The structure of our predictor is illustrated is as shown in
Figure 9.1. To build such a predictor, three
steps need to be carried out. The first is to form a database collected
from real traffic traces for a sufficiently long period and to format
this database in a specific manner (as described bellow). The second is
to identify a suitable NN architecture and training algorithm as
described in Sec. 9.3.3. Generally, the three-layer
feedforward network and any efficient training algorithm like the
Levenberg-Marquardt or the Conjugate Gradient algorithms may be a good
choice. The third step is to train and test this NN and to select a
retraining strategy (either periodically off line whenever the
performance degrades bellow certain predefined threshold, or on line),
see Sec. 9.3.6 for experimental results regarding
this point. Concerning the real traces, they should be collected from the
network whose traffic we want to predict. The accuracy of the method
will greatly depend on the network traffic used in this learning phase.
Each of the training and testing databases should consist of 5
parts. The first is the ``now window'' which consists of
 , where
, where  is the current value of the traffic and
is the current value of the traffic and
 represents the value of the
represents the value of the  previous step. The
second part is the ``yesterday window'', which contains
previous step. The
second part is the ``yesterday window'', which contains
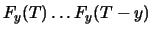 , where
, where  is the value of the traffic yesterday at the
same time as now, and
is the value of the traffic yesterday at the
same time as now, and 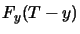 is that of
is that of 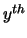 previous
step. Similarly, the third part is the ``week window'', which contains
previous
step. Similarly, the third part is the ``week window'', which contains
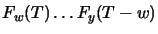 , where
, where  is the value of the traffic in
the previous week, in the same day and at the same time as
now.
is the value of the traffic in
the previous week, in the same day and at the same time as
now. 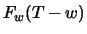 is that of
is that of 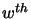 previous step. Then come the
``day'' and ``date'', where the ``day'' represents the day of the week
from 0 to 6, and the ``time'' represents the time of the day. The
``time'' variable takes discrete values depending on the ``step size''.
For example, if the ``step size'' is one minute, the ``time'' takes
values that vary from 0 to
previous step. Then come the
``day'' and ``date'', where the ``day'' represents the day of the week
from 0 to 6, and the ``time'' represents the time of the day. The
``time'' variable takes discrete values depending on the ``step size''.
For example, if the ``step size'' is one minute, the ``time'' takes
values that vary from 0 to 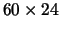 . The final part is the next
value of the traffic,
. The final part is the next
value of the traffic,  , that is, the output of the NN. All these data should be normalized to the range from 0 to 1. This is to achieve better performance, see Sec. 9.3.2 for more details. The ``now window'' represents the short-term information of the traffic process. Both the ``day window'' and ``week window'' as well as the ``day'' and ``date'' represent the long-term information.
, that is, the output of the NN. All these data should be normalized to the range from 0 to 1. This is to achieve better performance, see Sec. 9.3.2 for more details. The ``now window'' represents the short-term information of the traffic process. Both the ``day window'' and ``week window'' as well as the ``day'' and ``date'' represent the long-term information.
Figure 9.1:
A black-box representation of our tool to predict in real time
the future traffic, where
![$T\in[0,\infty]$](img385.gif) is the time step number,
is the time step number,  is the current value of the traffic,
is the current value of the traffic,
 is that at the previous
is that at the previous  step,
step,  is that in the
same instant but yesterday,
is that in the
same instant but yesterday,  is that in the previous week,
``Time'' is the discrete time of the day, and ``Day'' is the day of
the week
is that in the previous week,
``Time'' is the discrete time of the day, and ``Day'' is the day of
the week
|
|





Next: Experimental Results and Evaluation
Up: Using Neural Networks for
Previous: Introduction
Contents
Index
Samir Mohamed
2003-01-08
![\fbox{\includegraphics[width=.6\textwidth]{TrafficFigs/Model.eps}}](img65.gif)
![\fbox{\includegraphics[width=.6\textwidth]{TrafficFigs/Model.eps}}](img65.gif)