| Segmentation
of brain structures |
Contact: Caroline
Baillard, Pierre Hellier
, Christian Barillot
Introduction
Segmentation
based on level sets
formalism
propagation force
adaptive step
Cooperation
with the registration process
Experimental results
We propose a cooperative strategy for the segmentation of 3D brain MRI
which integrates 3D segmentation and 3D registration methods. The segmentation
method is based on Level Set formalism. A closed 3D surface representing
the structure of interest starts from an initial position and iteratively
propagates towards the desired boundaries through the evolution of a 4D
implicit function. The contribution of this work is three-fold. First,
we use an automatic registration method to initialize the surface as an
alternative to manual initialization. The volume to be segmented is registered
against a reference volume (of known segmentation) through a robust multi-resolution
and multi-grid minimization scheme. The initial location provided by the
registered reference volume allows the segmentation to be faster and fully
automatic. Second, a bi-directional propagation force is designed based
on local intensity values, allowing the surface to extend or contract locally.
Third, an adaptive iteration step is employed for the computation of the
evolving surface. Whereas manual tuning has typically been employed to
trade off speed of convergence against stability, we propose automatically
evaluating an optimal step value at each iteration in order to improve
the robustness and the efficiency of the algorithm.
| Segmentation
based on level sets |
The segmentation problem is expressed as the computation of a 3D surface
(or front) propagating in time along its normal direction. In the level
set formulation, the propagating front is embedded as the zero level of
a time-varying higher dimensional function:
This4-D surface is defined by the signed distance from X to the
surface. It is shown that the evolution rule can be expressed as:
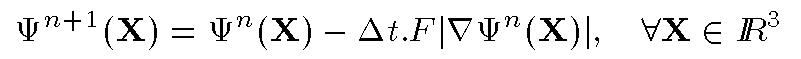
The 4D surface deforms iteratively according to a speed function
F,and
the position of the 3D front is deduced from it at each iteration step.
The parameter F is a scalar velocity function which depends on local
properties of the front like the local curvature, and on external parameters
related to the input data or expressing an additional propagation force.
The design of the speed function is a key point of the segmentation.
Osher and Setian suggest the following:
where h(I) is related to the image intensity and acts as a stopping
criterion at the location of the desired boundaries, k represents
the local curvature of the front and acts as a regularization term, and
v
represents
an additional propagation force which eithercontracts or expands the surface.
Previous approaches to 3D segmentation using this model have imposed a
one-way propagation force, which either contracts or expands the whole
surface all along the process. However, when the initial position of the
surface can be predicted, it is necessary to let the surface evolve in
both directions (since predicted and real positions usually overlap). Some
models have been proposed to solve this problem in 2D. In the last equation,
the sign of v determines the direction of the external propagation
force. We propose to locally determine this sign by using local intensity
values.
The iteration step dt of the first equation
is usually constant and manually tuned. We propose to compute it automatically
at each iteration in order to get the best efficiency. The stability of
the process requires a numerical scheme for the computation of the hypersurface,
called upwind sheme. The stability is then guaranteed only if the
iteration step dt is limited.
We use the optimal value of dt given by:
Where Hu, Hv, Hw are the partial derivatives of the Hamiltonian
H defined by:
| Cooperation
with the registration process |
The association of the adaptive step with the narrow band technique
considerably speeds up the segmentation. The narrow band technique consists
of updating the hypersurface only at points located in a narrow band around
the front. However the processing time can be even more reduced if a close
and adaptive initialization is provided. Furthermore, the segmentation
becomes fully automatic as soon as the initialization is automatic. In
this context information provided by the registration process explained
here
is of prime interest.
Let suppose that we have N volumes to segment. A reference volume
Vo
is chosen and segmented with a manual initialization (a small cube inside
the object for instance). Every new volume Vi (or target) is first
registered with the reference one Vo using the registration method,
which provides a dense deformation field (from Vo to Vi).
The segmented structure in the reference volume Vo is then deformed
by this field in order to predict the location of the structure in the
target volume Vi. This predicted location is used for initializing
the segmentation process.
Ventricle segmentation (orange) for two different subjects. The first
row shows a subpart of the reference volume (original size 256.256.176)
segmented in 620 iterations; the surface was manually initialized with
a cube of size 5.5.5 located inside the ventricles. The second row shows
the target volume segmented in 170 iterations; the surface was automatically
initialized using registration and the result of the first row. The three
columns respectively show axial, coronal and saggital planes.
Ventricules detected in the reference volume projected onto the target
volume, before registration (orange) and after registration (red).
Brain segmentation (orange) for two different subjects. First row:
reference volume segmented in 980 iterations (manual initialization with
a cube of size 40.80.40). Second row: target volume segmented in 240 iterations
(automatic initialization by registration with the reference volume). The
three columns respectively show axial, coronal and saggital planes.
3D views of the segmented ventricles (left) and brain (right) from
the target volume.
-
Caroline Baillard, Pierre Hellier, Christian Barillot, Segmentation
of 3D brain structures using level sets. Rapport interne IRISA No 1291,
January 2000.
