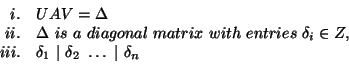
![]() is unique
and is called the Smith normal form of
is unique
and is called the Smith normal form of ![]() .
.
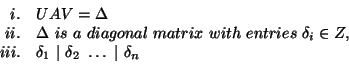
![]() is unique
and is called the Smith normal form of
is unique
and is called the Smith normal form of ![]() .
.
For example, consider the matrix:
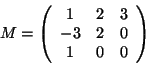
Its Smith normal decomposition is:
![]() where:
where:
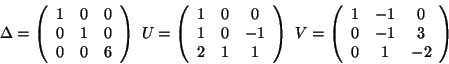
In [NRi00], and affine smith normal form has been defined for affine matrices. The corresponding function in Polylib is: