EP-ATR

Exemple Chat/Souris

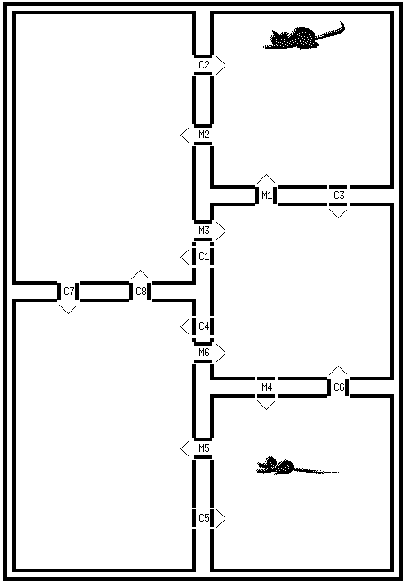
Dans Wonham.al87 , Wonham et Ramadge ont présenté un problème de contrôle d'un système à événements discrets. Un chat et une souris vivent dans le labyrinthe matérialisé par la figure ci-dessous.

Modèle de la maison (Cliquez pour agrandir)

Le labyrinthe comporte 5 pièces numérotées de 0 à 4, les animaux passent d'une pièce à l'autre en franchissant des portes symbolisées par des flèches dans la figure ci-dessus. Les portes M1 à M6 ne sont franchissables que par la souris, les portes C1 à C7 que par le chat. à l'exception de la porte C7, chaque porte ne peut être franchie que dans un seul sens.

Un dispositif de contrôle permet d'ouvrir et de fermer le portes M1 à M6 et C1 à C6. La porte C7 est quant à elle toujours ouverte. Un capteur est associé à chaque porte, et en signale le franchissement. Initialement, le chat est dans la pièce 2 et la souris dans la pièce 4. Le dispositif est commandé de manière à assurer les deux objectifs suivants :

(1) Le chat et la souris ne se rencontrent jamais.

(2) Ils peuvent toujours revenir à la position initiale .

(3) Le contrôleur doit laisser le maximum de liberté de mouvement aux animaux.

Le modèle physique (dans lequel on retrouve l'état des pièces et des portes) à été décrit dans le langage SIGNAL

Modèle physique spécifié en Signal (Cliquez pour agrandir)

Exemple : modélisation de l'état des pièces pour la souris en fonction du mouvement de la souris et de l'état des portes.

Pour compléter le modèle, nous avons rajouté des assertions sur les mouvements des animaux (qui traduisent l'impossiblité pour les animaux de faire deux mouvements différents simultanément et de choisir un mouvement alors qu'ils sont dans la mauvaise pièce. Par exemple, il semble impossible que le chat veuille bouger de la pièce 0 vers la pièce 1, si il ne se trouve pas au préalable dans cette pièce et si la porte correspondante n'est pas ouverte.).

Assertions sur les événements contrôlables
et incontrôlables (Cliquez pour agrandir)

Exemple : Assertions faites sur les mouvements possible du chat.

Les objectifs de commandes ont alors été exprimés en signal+ comme décrit par la figure suivante :

Description des objectifs de commande (Cliquez pour agrandir)

Le système dans sa globalité a ensuite été traduit en termes de systèmes dynamiques polynomiaux afin de pouvoir réaliser (en utilisant SIGALI) la synthèse des trois objectifs de commandes décrits plus haut. Une fois le contrôleur calculé, celui-ci a été intégré dans l'environnement SIGNAL en vue de la simulation. Cet exemple à donné lieu à une interface graphique représentée par le schéma ci-dessous.