La figure montre comment circulent les chariots dans l'usine (celle-ci est modélisée dans cet exemple par un réseau de Petri). 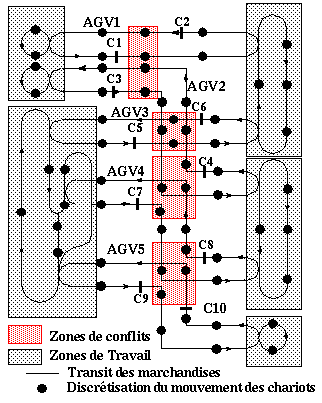 Schéma de principe du problème des chariots filoguidés dans une usine Le but du problème est de synthétiser un contrôleur responsable de la conduite de ces chariots. Il doit faire en sorte que deux chariots ne puissent se trouver en même temps dans une des 4 zones de conflits. On suppose que le contrôleur reçoit de la part de chaque chariot sa position courante, permettant au contrôleur de connaître à chaque instant l'état global du système. On suppose de plus que le contrôleur peut stopper les chariots avant leur entrée dans les zones de conflits par l'intermédiaire des commandes Ci. L'objectif de ce problème est donc de générer un contrôleur le
plus permissif possible qui fasse en sorte que les chariots ne se
rencontrent pas dans les zones de conflits tout en gardant un maximum
de liberté dans leurs mouvements.
Nous supposons dans un premier temps, qu'il y a un unique chariot par zone de déplacement. Afin de rendre le plus général possible la spécification de l'usine, le système est décomposé en 10 sous-systèmes, représentant respectivement les 5 stations de travail et les 5 zones de déplacement. Chaque sous-système peut alors être représenté par un réseau de Petri assez simple ayant au maximum 15 états (processus WORK_STATION_i pour les stations de travail et AGV_i pour les zones de déplacement). Le mouvement dans chaque sous-système est cadencé par une horloge propre à chacun (Time_WST_i pour les mouvements dans les stations de travail et Time_AGV_i pour les mouvements des chariots dans les zones de déplacement). Enfin des échanges d'informations entre chaque sous-système forcent la synchronisation entre ceux-ci. 
Modélisation Signal programme des chariots filoguidés (Cliquez pour agrandir) Afin de réaliser nos objectifs de commande, il convient de définir les états du système où deux chariots sont dans la même zone de conflits (on parlera d'états interdits). Ce processus, décrit par la figure suivante est écrit en signal+. Un premier sous-processus sert à spécifier les ensembles d'états interdits. Par exemple, le signal Conflit_area_1 est un booléen qui est vrai lorsque le chariot de la zone de déplacement 1 et le chariot de la zone de déplacement 2 sont tous les deux dans la zone de conflit 1. 
Processus Signal+ Décrivant les objectifs de commandes (Cliquez pour agrandir) Chacune des zones de conflits est ainsi décrite en Signal. Finalement le booléen Conflict_Area est vrai lorsque l'un des booléens codant l'occupation de chaque zone de conflits est vrai. Il correspond à l'ensemble des états interdits. Dans le deuxième processus, écrit en Signal+, les variables contrôlables sont déclarées ainsi que les objectifs de commande et de vérification. Par exemple, la commande SIGALI(S_Security(B_False(Conflict_Area))) va synthétiser un contrôleur rendant invariant sous contrôle l'ensemble des états permis (ie, le complémentaire logique des états interdits), interdisant ainsi à deux chariots de se trouver dans une même zone de conflit en même temps. la directive SIGALI(S_Free_Max()) renforce le contrôleur
précédemment calculé en forçant les commandes choisies de manière
à ce que les mouvements incontrôlables soient le plus libre possible
(ie, le mouvement des chariots). Finalement, la directive
SIGALI(REACHABLE(B_True(Conflict_Area))) permet de vérifier
par la suite que les états interdits sont devenus inaccessibles
pour le système contrôlé.
Après décompilation du programme Signal complet (modèle physique + objectifs de commande et de vérification) en un système dynamique polynomial, un fichier Controller_CMD.z3z est créé. Ce fichier a l'allure suivante : 
fichier Controller_CMD.z3z généré lors de la compilation sous format z3z du programme Signal (Cliquez pour agrandir) Il ne reste alors plus qu'à charger ce fichier dans SIGALI. La synthèse du contrôleur et la vérification de la propriété sont réalisées automatiquement. La visualisation des résultats se fait en lisant le fichier Controller.log. L'avant dernière ligne du fichier Controller_CMD.z3z permet de stocker le contrôleur obtenu en vue de la simulation. Finalement, une simulation du système contrôlé est obtenu. 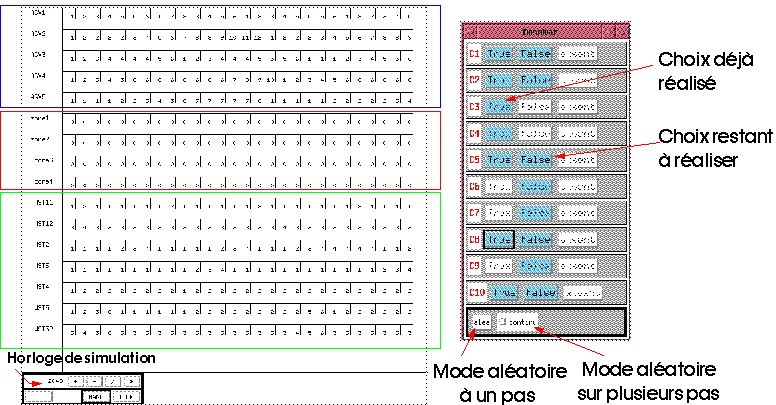
Simulation du programme des chariots filoguidés contrôlé (Cliquez pour agrandir)
L'utilisateur a la possibilité par l'intermédiaire de la boite resolver de choisir si il veut stopper un chariot. Le resolveur lui indique si son choix est valide ou non et lui renvoie les conséquences de son choix sur les commandes restants à choisir.
|
||||
|
|